题目
MAT137Y1 LEC 20249: Calculus with Proofs (all lecture sections) Pre-Class Quiz 49 (10.2)
单项选择题
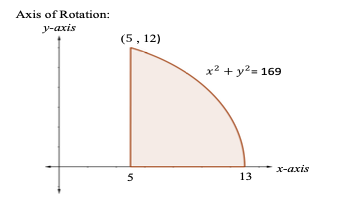
Let S be the solid of revolution obtained by rotating the shaded region in the figure below about the line y=-1. This region is bounded by x=5, y=0 and the curve 𝑥 2 + 𝑦 2 = 169 . Which two of the following definite integrals give the volume of S? I. ∫ 0 12 2 𝜋 ( 𝑦 + 1 ) 169 − 𝑦 2 𝑑 𝑦 II. ∫ 0 12 2 𝜋 𝑦 ( 169 − 𝑦 2 − 5 ) 𝑑 𝑦 III. ∫ 5 13 𝜋 ( 2 169 − 𝑥 2 + 169 − 𝑥 2 ) 𝑑 𝑥 IV. 𝜋 ∫ 5 13 ( 169 − 𝑥 2 + 1 ) 2 𝑑 𝑥 V. ∫ 0 12 2 𝜋 ( 𝑦 + 1 ) ( 169 − 𝑦 2 − 5 ) 𝑑 𝑦
选项
A.I and IV
B.II and V
C.III and V
D.II and IV
E.I and III
查看解析
标准答案
Please login to view
思路分析
We start by restating the scenario and listing the given options to keep the analysis clear.
Question restated: The region shaded is bounded by x = 5, y = 0, and the circle x^2 + y^2 = 169. The solid S is formed by rotating this region about the horizontal line y = -1. We are asked which two definite integrals among I–V compute the volume of S.
Answer options:
I. ∫_0^{12} 2π (y + 1) (169 − y^2) dy
II. ∫_0^{12} 2π y (169 − y^2 − 5) dy
III. ∫_5^{13} π [ (2(169 − x^2) + (169 − x^2) ) ] dx
IV. π ∫_5^{13} (169 − x^2 + 1)^2 dx
V. ∫_0^{12} 2π (y + 1) (169 − y^2 − 5) dy
To analyze, pick a suitable method. The region is better handled with horizontal slices (constant y) because the axis of rotation is horizontal (y = -1). For a slice at a fixed y, the radius of rotation is the distance from y to -1, which is y + 1. The slice’s horizontal extent runs from x = 5 ......Login to view full explanation登录即可查看完整答案
我们收录了全球超50000道考试原题与详细解析,现在登录,立即获得答案。
类似问题
The area bounded by the curve \( y=2sin(2x) \), the y-axis and the line y = 2 is rotated about the x-axis. The volume formed is equal to:
The area bounded by the curve y=2sin(2x)[math] y=2sin(2x) , the y-axis and the line y = 2 is rotated about the x-axis. The volume formed is equal to:
Question textThe volume of the solid of revolution formed by rotating the curve \(y=\text{Arcsin}(\frac{x}{2}), 0\leq x\leq 2\) about the \(y\)-axis is Answer 1 Question 34[input]\(\pi^2\).
Question textThe volume generated by rotating, about the \(X\) axis, the region enclosed by \(y=x^{\frac{3}{2}}\), \(x=1,x=2\), and the \(X\) axis, is Answer 1 Question 5[input] \(\pi \big/\) Answer 2 Question 5[input].
更多留学生实用工具
希望你的学习变得更简单
加入我们,立即解锁 海量真题 与 独家解析,让复习快人一步!