题目
MUF0102 Adv. Mathematics Unit 2 - Semester 2, 2025 3.8 Applications of calculus quiz
单项选择题
The area bounded by the curve \( y=2sin(2x) \), the y-axis and the line y = 2 is rotated about the x-axis. The volume formed is equal to:
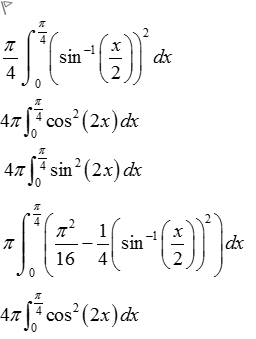
查看解析
标准答案
Please login to view
思路分析
The problem asks for the volume generated when the region bounded by the curve y = 2 sin(2x), the y-axis (x = 0), and the horizontal line y = 2 is rotated about the x-axis.
First, determine the x-limits: the curve reaches y = 2 when 2 sin(2x) = 2, so sin(2x) = 1, which gives 2x = π/2......Login to view full explanation登录即可查看完整答案
我们收录了全球超50000道考试原题与详细解析,现在登录,立即获得答案。
类似问题
The area bounded by the curve y=2sin(2x)[math] y=2sin(2x) , the y-axis and the line y = 2 is rotated about the x-axis. The volume formed is equal to:
Question textThe volume of the solid of revolution formed by rotating the curve \(y=\text{Arcsin}(\frac{x}{2}), 0\leq x\leq 2\) about the \(y\)-axis is Answer 1 Question 34[input]\(\pi^2\).
Question textThe volume generated by rotating, about the \(X\) axis, the region enclosed by \(y=x^{\frac{3}{2}}\), \(x=1,x=2\), and the \(X\) axis, is Answer 1 Question 5[input] \(\pi \big/\) Answer 2 Question 5[input].
Question textThe volume of the solid of revolution formed by rotating the curve \(y=\text{Arcsin}(\frac{x}{2}), 0\leq x\leq 2\) about the \(y\)-axis is Answer 1 Question 4[input]\(\pi^2\).
更多留学生实用工具
希望你的学习变得更简单
加入我们,立即解锁 海量真题 与 独家解析,让复习快人一步!