题目
FNDN 2025 O1 Challenge Week 2 Examinations
单项选择题
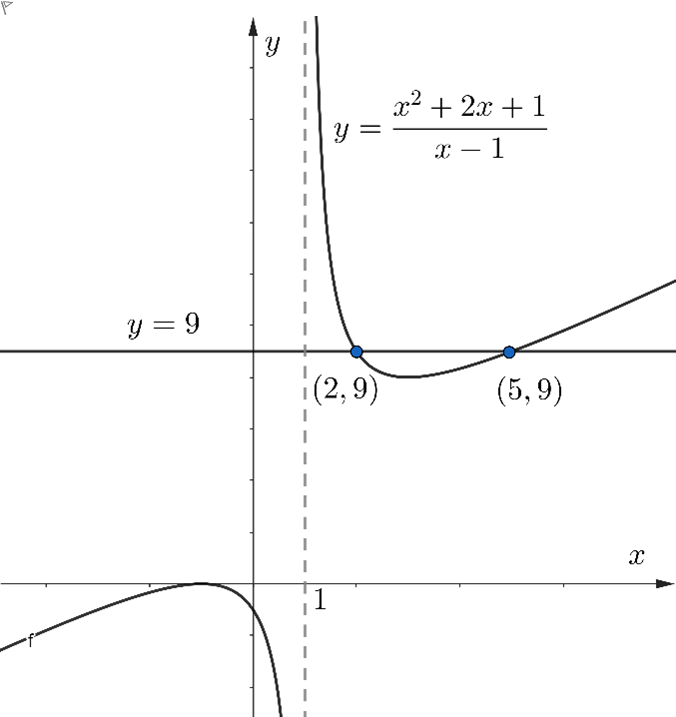
The graphs of the line [math: y=9] and the curve [math: y=x2+2x+1x−1]y=\dfrac{x^2+2x+1}{x-1} intersect at the points [math: (2,9)](2, 9) and [math: (5,9)](5, 9) , as shown in the diagram below. State the solution to the inequality [math: x2+2x+1x−1≤9]\dfrac{x^2+2x+1}{x-1}\leq 9 .
选项
A.[math: 2≤x≤5]2 \leq x \leq 5
B.[math: 1<x≤2 or x≥5]1\lt x \leq 2 \text{ or } x\geq 5
C.[math: x<1]x \lt 1
D.[math: x<1 or 2≤x≤5]x\lt 1 \text{ or } 2 \leq x\leq 5
查看解析
标准答案
Please login to view
思路分析
We begin by translating the given inequality into a rational inequality that we can analyze piece by piece.
Option analysis often hinges on identifying critical points where the expression changes sign or becomes undefined.
First, rewrite the expression: y = (x^2 + 2x + 1)/(x - 1) ≤ 9. Notice the numerator factors as (x + 1)^2, so we have (x + 1)^2/(x - 1) ≤ 9.
To bring everything to one side, subtract 9 from both sides: (x + 1)^2/(x - 1) - 9 ≤ 0. Get a common denominator to combine: [(x + 1)^2 - 9(x - 1)]/(x - 1) ≤ 0.
Expanding the numerator yields (x^2 + 2x + 1) - 9x + 9 = x^2 - 7x + 10,......Login to view full explanation登录即可查看完整答案
我们收录了全球超50000道考试原题与详细解析,现在登录,立即获得答案。
类似问题
Question textThe students below solved rational inequalities. Match each student’s reasoning to the best explanation.Student 1:“I solved \frac{1}{x+1} < 5 and wrote the solution intervals as x < -1 or x > -\frac{4}{5} .” Answer 1 Question 22[select: , The student found the correct critical points but only x < -1 is a valid interval; x > -4/5 is not valid., The student listed the correct critical points but mistakenly concluded the interval solution; the correct solution is -1 < x < -4/5., The student correctly solved the inequality and gave appropriate solution intervals using the correct critical points.]Student 2:“I solved \frac{2x}{x-1} > 3 and wrote x > 3 as my solution interval.” Answer 2 Question 22[select: , The student correctly identified the critical points and the solution; the correct interval is x > 3., The student identified the correct critical points, but the solution is incorrect; the correct solution is x < 1, x > 3., The student identified the correct critical points but the solution is incorrect; the correct solution is 1 < x < 3. ]Student 3:“I solved \frac{x+4}{x-3} < 2 and listed critical points at x = -4 and x = 3 .” Answer 3 Question 22[select: , The student correctly listed the critical values as x = -4 and x = 3., The student attempted to identify critical points but incorrectly listed x = -4; the correct critical points are x = 3 and x = 10., The student attempted to identify critical points but incorrectly listed x = -4 instead of x = 2; the correct critical points are x = 3 and x = 2.]
Which of the following intervals are part of the solution set of x 2 − 3 x − 4 x 2 − x − 2 ≥ 0 ? {"version":"1.1","math":"\dfrac{x^2-3x-4}{x^2-x-2}\ge 0?"}
Consider the inequalities:[math: d1:(x−1)(x+3)≥0] d_1: \quad (x-1)(x+3) \ge 0 [math: d2:x−1x+3≥0] d_2: \quad \frac{x-1}{x+3} \ge 0
In a consumer society, many adults channel creativity into buying things
更多留学生实用工具
希望你的学习变得更简单
加入我们,立即解锁 海量真题 与 独家解析,让复习快人一步!