题目
COMP 543 001 Quiz 4
单项选择题
In class, I asserted that is the same as , where and are predicates. That is, you can "not" or "negate" a predicate that is itself a conjunction of predicates by distributing the "not" over the inner predicates, and changing the "and" to an "or". Using this rule, and the fact that is equivalent to and also that is equivalent to , we can argue that can be re-written as what?
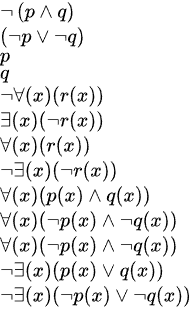
查看解析
标准答案
Please login to view
思路分析
The prompt asks us to rewrite the negation of a conjunction of predicates using the given logical equivalences, but the provided data has no answer options to analyze. I will nevertheless walk through the correct transformation and point out common missteps that might appear.
First, recall De Morgan’s law for predicates: not (A and B) is equivalent to (not A) or (not B). When the domain involves a ......Login to view full explanation登录即可查看完整答案
我们收录了全球超50000道考试原题与详细解析,现在登录,立即获得答案。
类似问题
Formulate two distinct logical predicates that accurately represent the following new information: “News247 is a news application that has a rating of 8.” The predicates should follow to the previously established syntax and representation schema of the knowledge base. (6 marks)
A predicate can be described as… (Pick the statement that applies.)
Which of the following is not an example of a predicate?
Suppose isPositive(X) evaluates to True when X is a positive number, and False otherwise. If X = -2, which of the following is not true about isPositive(X)?
更多留学生实用工具
希望你的学习变得更简单
加入我们,立即解锁 海量真题 与 独家解析,让复习快人一步!