题目
SPHY001 Practice Quiz - Unit 10 | LA050
单项选择题
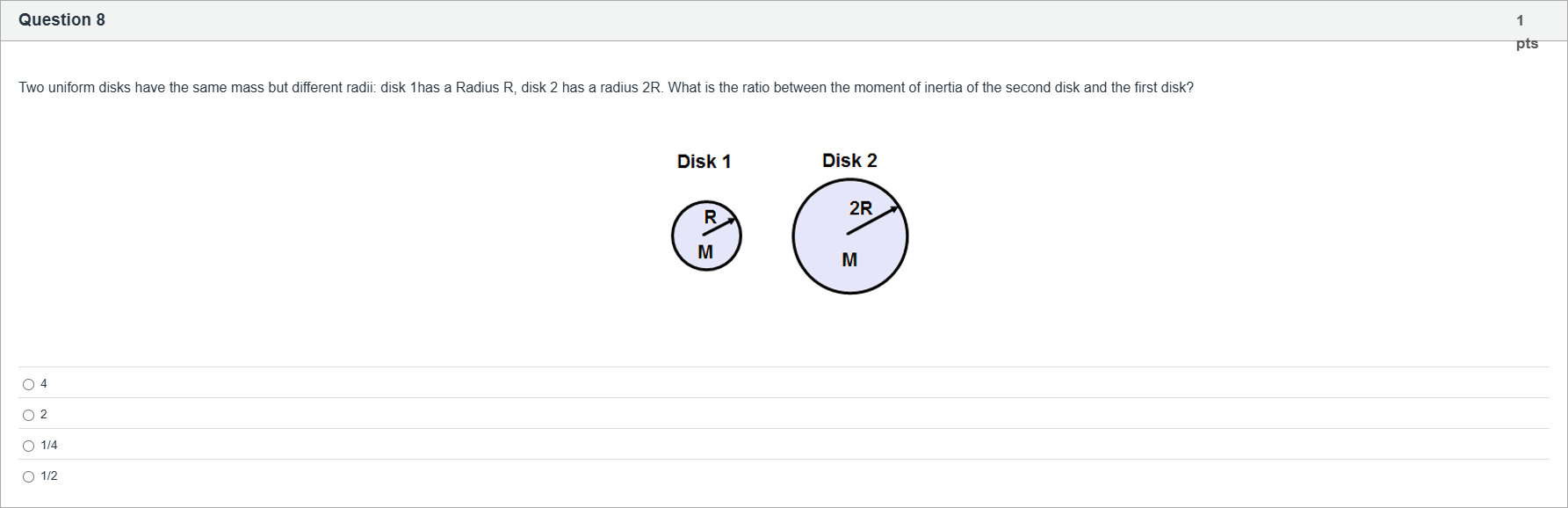
Two uniform disks have the same mass but different radii: disk 1has a Radius R, disk 2 has a radius 2R. What is the ratio between the moment of inertia of the second disk and the first disk?
选项
A.4
B.2
C.1/4
D.1/2
查看解析
标准答案
Please login to view
思路分析
Let’s parse the problem step by step and compare the moments of inertia for the two disks.
Disk 1 has radius R and Disk 2 has radius 2R, with both having the same mass M. For a uniform disk, the moment of inertia ......Login to view full explanation登录即可查看完整答案
我们收录了全球超50000道考试原题与详细解析,现在登录,立即获得答案。
类似问题
A 1.2kg mass is located at the origin of an xy coordinate system, a 2.5 kg mass is at x = 2m, y = 0, and a 9kg mass at x = 0, y = 1m. For this arrangement of the three masses, what is the angular acceleration of the system if a torque τ rotates the system about the y axis? All answers in inverse seconds squared.
Question text1. The water volume of the Aral sea was 1093 km3[math] in 1960, and decreased exponentially to 102 km3[math] in 2009. The density of salty water is about 1020 kg/m3[math]. a) Calculate the mass of water lost by the Aral sea from 1960 until 2009. Approximate your answer to 3 significant figures and give the answer in kg. Answer 1 Question 7[input] ×1015kg[math] b) Assume that the mass of the lost water was 9.09×1014[math] kg and that it was evaporated and redistributed over the surface of Earth as a homogeneous thin spherical shell. This change in mass distribution will result in a change in Earth’s moment of inertia. Assume that initially the lake had all its mass concentrated at a point with coordinates 45°N 60°E (a point mass approximation). Calculate the change in Earth’s moment of inertia due to the redistribution of Lake Aral’s water. Give the answer in kgm2[math] to 3 significant figures (be careful with the sign of the final answer). You may use: -Moment of inertia of homogeneous thin spherical shell with mass M and radius R is: I=(2/3)MR2[math] -Moment of inertia of point mass with mass M and distance r from axis of rotation is: I=Mr2[math] -Radius of Earth=6371 km Answer 2 Question 7[input] ×1027kgm2[math]c) Assume the moment of inertia of Earth in 1960 to be 8.04×1037kgm2[math] and that the change in moment of inertia due to Aral's water evaporation was 6.77×1027kgm2[math]. Conservation of angular momentum tells us that: Iinitial/Tinitial=Ifinal/Tfinal[math] Where I[math] and T[math] are the moment of inertia and Earth’s period of rotation about its own axis (24 hours). Calculate in microseconds the expected change in Earth’s rotation period. Approximate to 2 significant figures.Answer 3 Question 7[input] μs[math]
Question text1. The water volume of the Aral sea was 1093 [math: km3] in 1960, and decreased exponentially to 102 [math: km3] in 2009. The density of salty water is about 1020 [math: kg/m3]. a) Calculate the mass of water lost by the Aral sea from 1960 until 2009. Approximate your answer to 3 significant figures and give the answer in kg. Answer 1 Question 7[input] [math: ×1015kg] b) Assume that the mass of the lost water was [math: 9.09×1014] kg and that it was evaporated and redistributed over the surface of Earth as a homogeneous thin spherical shell. This change in mass distribution will result in a change in Earth’s moment of inertia. Assume that initially the lake had all its mass concentrated at a point with coordinates 45°N 60°E (a point mass approximation). Calculate the change in Earth’s moment of inertia due to the redistribution of Lake Aral’s water. Give the answer in [math: kgm2] to 3 significant figures (be careful with the sign of the final answer). You may use: -Moment of inertia of homogeneous thin spherical shell with mass M and radius R is: [math: I=(2/3)MR2] -Moment of inertia of point mass with mass M and distance r from axis of rotation is: [math: I=Mr2] -Radius of Earth=6371 km Answer 2 Question 7[input] [math: ×1027kgm2]c) Assume the moment of inertia of Earth in 1960 to be [math: 8.04×1037kgm2] and that the change in moment of inertia due to Aral's water evaporation was [math: 6.77×1027kgm2]. Conservation of angular momentum tells us that: [math: Iinitial/Tinitial=Ifinal/Tfinal] Where [math: I] and [math: T] are the moment of inertia and Earth’s period of rotation about its own axis (24 hours). Calculate in microseconds the expected change in Earth’s rotation period. Approximate to 2 significant figures.Answer 3 Question 7[input] [math: μs]
Two uniform disks have the same mass but different radii: disk 1has a Radius R, disk 2 has a radius 2R. What is the ratio between the moment of inertia of the second disk and the first disk?
更多留学生实用工具
希望你的学习变得更简单
加入我们,立即解锁 海量真题 与 独家解析,让复习快人一步!