题目
SPHY001 Practice Quiz - Unit 10 | LA050
单项选择题
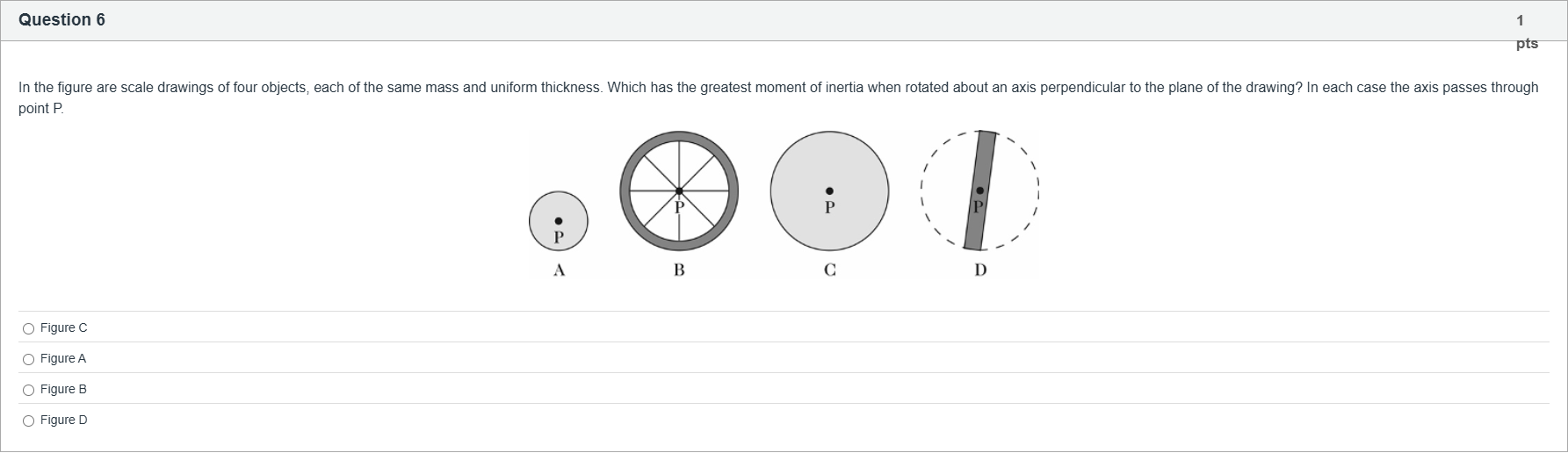
In the figure are scale drawings of four objects, each of the same mass and uniform thickness. Which has the greatest moment of inertia when rotated about an axis perpendicular to the plane of the drawing? In each case the axis passes through point P.
选项
A.Figure C
B.Figure A
C.Figure B
D.Figure D
查看解析
标准答案
Please login to view
思路分析
The question asks which object has the greatest moment of inertia about an axis perpendicular to the plane of the drawing, with the axis passing through point P in each figure. I will examine each option in turn and compare how the mass is distributed relative to P.
Option A: The small circle (A) appears to be a small disk with its center at P. For a disk rotating about its center, the moment of inertia is I = (1/2) m r^2, where r is the disk’s radius. Since this disk is small, both its radius and the average distance of mass elements from P are small, so its I......Login to view full explanation登录即可查看完整答案
我们收录了全球超50000道考试原题与详细解析,现在登录,立即获得答案。
类似问题
A 1.2kg mass is located at the origin of an xy coordinate system, a 2.5 kg mass is at x = 2m, y = 0, and a 9kg mass at x = 0, y = 1m. For this arrangement of the three masses, what is the angular acceleration of the system if a torque τ rotates the system about the y axis? All answers in inverse seconds squared.
Question text1. The water volume of the Aral sea was 1093 km3[math] in 1960, and decreased exponentially to 102 km3[math] in 2009. The density of salty water is about 1020 kg/m3[math]. a) Calculate the mass of water lost by the Aral sea from 1960 until 2009. Approximate your answer to 3 significant figures and give the answer in kg. Answer 1 Question 7[input] ×1015kg[math] b) Assume that the mass of the lost water was 9.09×1014[math] kg and that it was evaporated and redistributed over the surface of Earth as a homogeneous thin spherical shell. This change in mass distribution will result in a change in Earth’s moment of inertia. Assume that initially the lake had all its mass concentrated at a point with coordinates 45°N 60°E (a point mass approximation). Calculate the change in Earth’s moment of inertia due to the redistribution of Lake Aral’s water. Give the answer in kgm2[math] to 3 significant figures (be careful with the sign of the final answer). You may use: -Moment of inertia of homogeneous thin spherical shell with mass M and radius R is: I=(2/3)MR2[math] -Moment of inertia of point mass with mass M and distance r from axis of rotation is: I=Mr2[math] -Radius of Earth=6371 km Answer 2 Question 7[input] ×1027kgm2[math]c) Assume the moment of inertia of Earth in 1960 to be 8.04×1037kgm2[math] and that the change in moment of inertia due to Aral's water evaporation was 6.77×1027kgm2[math]. Conservation of angular momentum tells us that: Iinitial/Tinitial=Ifinal/Tfinal[math] Where I[math] and T[math] are the moment of inertia and Earth’s period of rotation about its own axis (24 hours). Calculate in microseconds the expected change in Earth’s rotation period. Approximate to 2 significant figures.Answer 3 Question 7[input] μs[math]
Question text1. The water volume of the Aral sea was 1093 [math: km3] in 1960, and decreased exponentially to 102 [math: km3] in 2009. The density of salty water is about 1020 [math: kg/m3]. a) Calculate the mass of water lost by the Aral sea from 1960 until 2009. Approximate your answer to 3 significant figures and give the answer in kg. Answer 1 Question 7[input] [math: ×1015kg] b) Assume that the mass of the lost water was [math: 9.09×1014] kg and that it was evaporated and redistributed over the surface of Earth as a homogeneous thin spherical shell. This change in mass distribution will result in a change in Earth’s moment of inertia. Assume that initially the lake had all its mass concentrated at a point with coordinates 45°N 60°E (a point mass approximation). Calculate the change in Earth’s moment of inertia due to the redistribution of Lake Aral’s water. Give the answer in [math: kgm2] to 3 significant figures (be careful with the sign of the final answer). You may use: -Moment of inertia of homogeneous thin spherical shell with mass M and radius R is: [math: I=(2/3)MR2] -Moment of inertia of point mass with mass M and distance r from axis of rotation is: [math: I=Mr2] -Radius of Earth=6371 km Answer 2 Question 7[input] [math: ×1027kgm2]c) Assume the moment of inertia of Earth in 1960 to be [math: 8.04×1037kgm2] and that the change in moment of inertia due to Aral's water evaporation was [math: 6.77×1027kgm2]. Conservation of angular momentum tells us that: [math: Iinitial/Tinitial=Ifinal/Tfinal] Where [math: I] and [math: T] are the moment of inertia and Earth’s period of rotation about its own axis (24 hours). Calculate in microseconds the expected change in Earth’s rotation period. Approximate to 2 significant figures.Answer 3 Question 7[input] [math: μs]
Two uniform disks have the same mass but different radii: disk 1has a Radius R, disk 2 has a radius 2R. What is the ratio between the moment of inertia of the second disk and the first disk?
更多留学生实用工具
希望你的学习变得更简单
加入我们,立即解锁 海量真题 与 独家解析,让复习快人一步!