你还在为考试焦头烂额?找我们就对了!
我们知道现在是考试月,你正在为了考试复习到焦头烂额。为了让更多留学生在备考与学习季更轻松,我们决定将Gold会员限时免费开放至2025年12月31日!原价£29.99每月,如今登录即享!无门槛领取。
助你高效冲刺备考!
题目
BU.520.601.T2.FA25 Final Exam
判断题
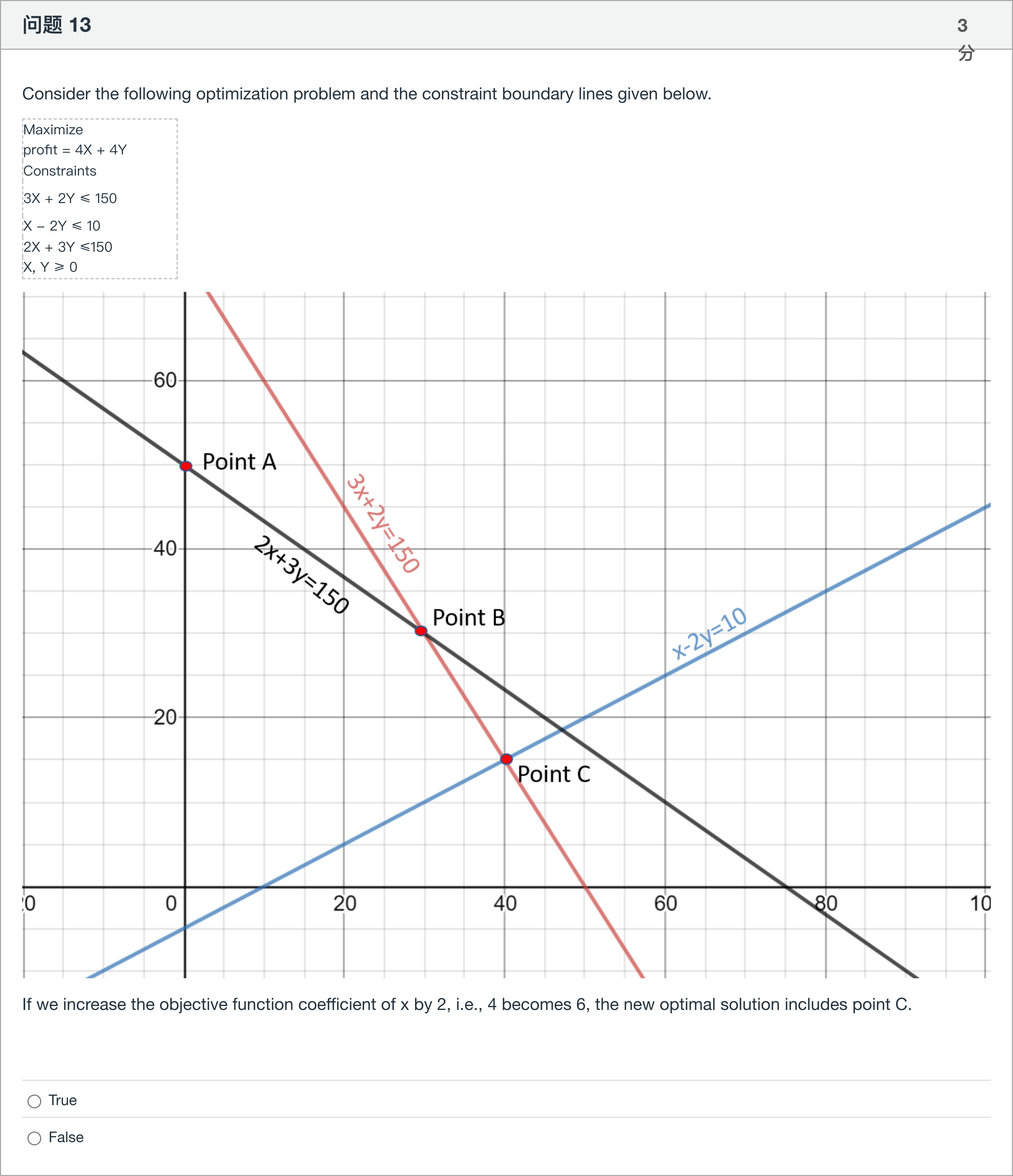
Consider the following optimization problem and the constraint boundary lines given below. Maximize profit = 4X + 4Y Constraints 3X + 2Y ≤ 150 X - 2Y ≤ 10 2X + 3Y ≤150 X, Y ≥ 0 If we increase the objective function coefficient of x by 2, i.e., 4 becomes 6, the new optimal solution includes point C.
选项
A.True
B.False
查看解析
标准答案
Please login to view
思路分析
Here is the problem restated: We have an optimization problem with Maximize profit = 4X + 4Y subject to the constraints 3X + 2Y ≤ 150, X − 2Y ≤ 10, 2X + 3Y ≤ 150, and X, Y ≥ 0. The statement claims that if we increase the objective function coefficient of x by 2 (from 4 to 6), the new optimal solution includes point C. The answer options are: True or False.
Option 1: True. This option asserts that increasing the coefficient of X in the objective function changes the optimal solution to include the point labeled C on the graph. To evaluate this, we consider how changing the objective coefficients affects the optimal vertex of the feasible region. When the profit coefficients change, the set of supporting hyperplanes (or iso-profit lines) rota......Login to view full explanation登录即可查看完整答案
我们收录了全球超50000道考试原题与详细解析,现在登录,立即获得答案。
类似问题
Solving a linear program can never result in integer values for the decision variables.
Consider the following optimization problem and the constraint boundary lines given below. Maximize profit = 4X + 4Y Constraints 3X + 2Y ≤ 150 X - 2Y ≤ 10 2X + 3Y ≤150 X, Y ≥ 0 When the constraint coefficient of x in the blue constraint changes from 1 to 3, the optimal solution changes.
Consider the following Excel sensitivity report and it's accompanying problem: Minimize cost = X + 2Y subject to X + 3Y ≥ 90 8X + 2Y ≥ 160 3X + 2Y ≥120 Y ≤ 70 X, Y≥ 0 Variable Cells Final Reduced Objective Allowable Allowable Cell Name Value Cost Coefficient Increase Decrease $B$3 X 25.71 0 1 2 0.333333333 $C$3 Y 21.43 0 2 1 1.333333333 Constraints Final Shadow Constraint Allowable Allowable Cell Name Value Price R.H. Side Increase Decrease $J$6 LHS 90 0.57 90 62 50 $J$7 LHS 248.57 0 160 88.57142857 1E+30 $J$8 LHS 120 0.14 120 150 28.18181818 $J$9 LHS 21.43 0 70 1E+30 48.57142857 Suppose we add another variable, x3, with an objective function coefficient of 9, and constraint coefficients of 8, 3, and 5 for the first three constraints, respectively. What is the marginal impact of this new variable on the objective function? (In your calculations round all the numbers to 2 decimals.)
A constraint is binding if it left hand side of a constraint is equal to the right hand side after the optimal solution is plugged into the constraint function.
更多留学生实用工具
希望你的学习变得更简单
为了让更多留学生在备考与学习季更轻松,我们决定将Gold 会员限时免费开放至2025年12月31日!