题目
MAT135H5_F25_ALL SECTIONS 2.2 Preparation Check
多项填空题
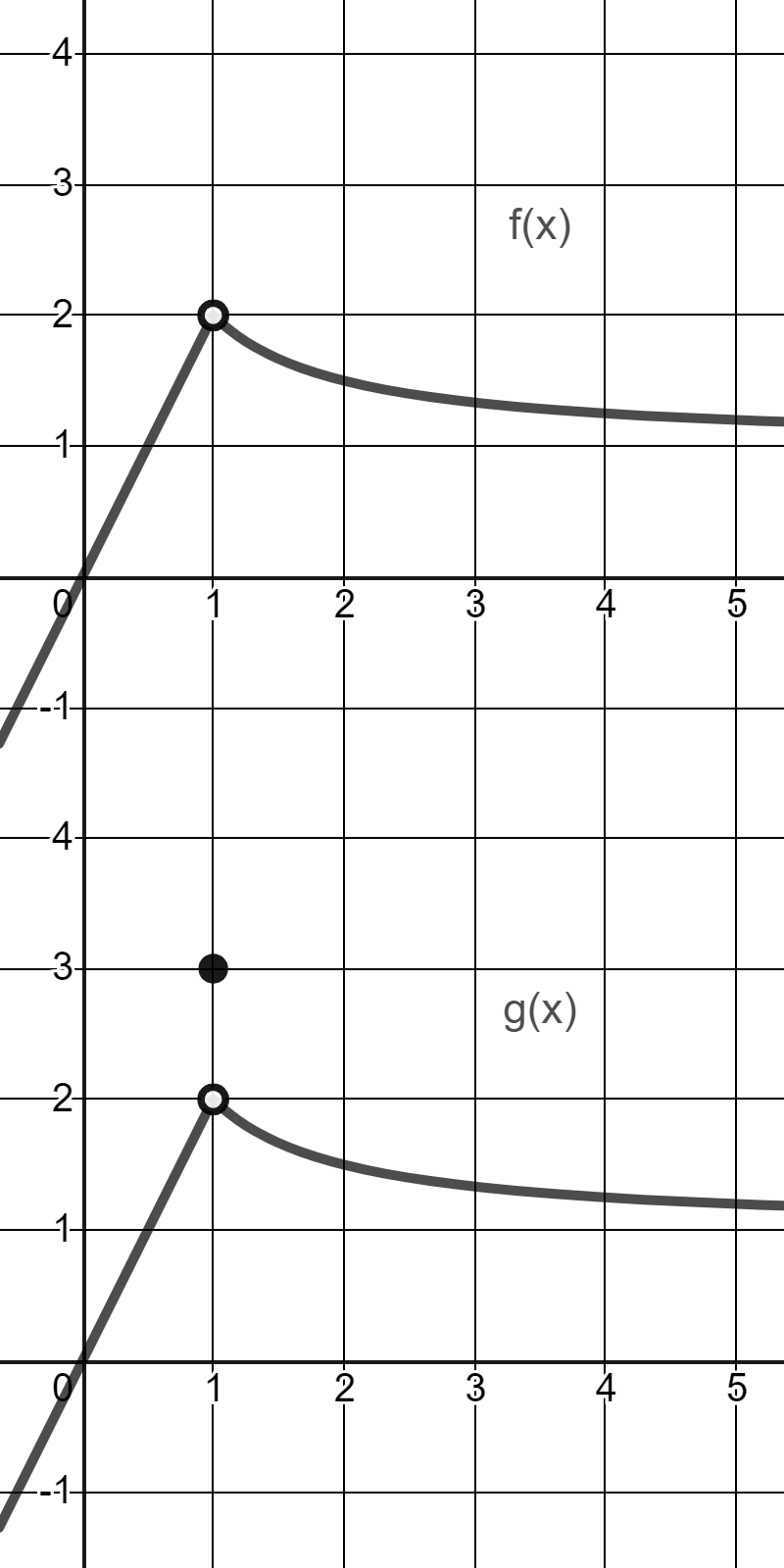
Consider the two graphs above. What are the following limits? (If a limit does not exist, write DNE.) limx→1f(x)=\lim\limits_{x\rightarrow1}f\left(x\right)= [Fill in the blank], limx→1g(x)=\lim\limits_{x\rightarrow1}g\left(x\right)= [Fill in the blank], Note that the two functions f(x)f\left(x\right) and g(x)g\left(x\right) are identical except for at x=1x=1 . Is the following statement TRUE or FALSE? For any function h(x)h\left(x\right) , the limit limx→ah(x)\lim\limits_{x\rightarrow a}h\left(x\right) does not depend on the value of h(x)h\left(x\right) at x=ax=a , or even whether h(a)h\left(a\right) is defined or not. [Fill in the blank], (Write "TRUE" or "FALSE".)
查看解析
标准答案
Please login to view
思路分析
To tackle the limits, I’ll describe what the graphs show as x approaches 1 for f(x) and g(x).
Option 1 (lim x→1 f(x) = 2): As x gets arbitrarily close to 1 from either side, the y-values of the curve f(x) approach the horizontal level y = 2. The graph indicates the function values near but not at x = 1 tend toward 2, even though the poin......Login to view full explanation登录即可查看完整答案
我们收录了全球超50000道考试原题与详细解析,现在登录,立即获得答案。
类似问题
Which of the following statements must be true, and which are false? Note: each part is independent from the others. a) If 𝑓 ( 𝑥 ) is a polynomial, then lim 𝑥 → 5 𝑓 ( 𝑥 ) can be evaluated by computing 𝑓 ( 5 ) . [ Select ] False True b) If 𝑅 ( 𝑥 ) is a rational function, then lim 𝑥 → 7 𝑅 ( 𝑥 ) can be evaluated by computing 𝑅 ( 7 ) . [ Select ] False True c) If 𝑝 ( 𝑥 ) is a polynomial, then lim 𝑥 → 5 + 𝑝 ( 𝑥 ) can be evaluated by computing 𝑝 ( 5 ) . [ Select ] True False d) If 𝑓 ( 2 ) = 4 then lim 𝑥 → 2 [ 𝑓 ( 𝑥 ) ] 2 = 16 [ Select ] False True e) If lim 𝑥 → 4 ( 5 𝑓 ( 𝑥 ) ) = 15 , then lim 𝑥 → 4 𝑓 ( 𝑥 ) = 3 . [ Select ] True False f) If lim 𝑥 → 4 ( 𝑥 𝑓 ( 𝑥 ) ) = 8 , then lim 𝑥 → 4 𝑓 ( 𝑥 ) = 2 . [ Select ] False True
the graph of f(x)f\left(x\right) given above. Use it to find the following one-sided and two-sided limits. (If a limit does not exist, write DNE.) limx→1−f(x)=\lim\limits_{x\:\rightarrow1^-}\:f\left(x\right)= [Fill in the blank], limx→1+f(x)=\lim\limits_{x\rightarrow1^+}f\left(x\right)= [Fill in the blank], limx→1f(x)=\lim\limits_{x\rightarrow1}f\left(x\right)\:= [Fill in the blank], limx→2f(x)=\lim\limits_{x\rightarrow2}f\left(x\right)= [Fill in the blank], limx→3−f(x)=\lim\limits_{x\rightarrow3^-}f\left(x\right)= [Fill in the blank], limx→3f(x)=\lim\limits_{x\rightarrow3}f\left(x\right)=[Fill in the blank], limx→4f(x)=\lim\limits_{x\rightarrow4}f\left(x\right)=[Fill in the blank],
Question text Consider the function [math: f(x)={3x+5,x<33x2+4x−2,x≥3] f(x)= \begin{cases} \displaystyle & {3\,x+5}, & x < {3} \\ & {3\,x^2+4\,x-2}, & x \geq {3}\end{cases} . a) [math: limx→3−f(x)=]\displaystyle \lim_{{x \to {3}^-}} f(x) = [input] b) [math: limx→3+f(x)=]\displaystyle\lim_{{x \to {3}^+}} f(x) = [input] c) [math: limx→3f(x)=]\displaystyle\lim_{{x \to {3}}} f(x) = [select: (Clear my choice), does not exist since left limit is not equal to right limit., exists and equals 37] Check Question 3
Question text Consider the graph of [math: f(x)] shown below: a) [math: limx→2−f(x)=]\displaystyle \lim_{{x \to {2}^-}} f(x) =[input] b) [math: limx→2+f(x)=]\displaystyle\lim_{{x \to {2}^+}} f(x) =[input] c) [math: limx→2f(x)=]\displaystyle\lim_{{x \to {2}}} f(x) =[select: (Clear my choice), does not exist., exists and equals 1] Check Question 1
更多留学生实用工具
希望你的学习变得更简单
加入我们,立即解锁 海量真题 与 独家解析,让复习快人一步!