题目
COMP9417-Machine Learning & Data Mining - T3 2025
多项选择题
Consider the following dataset: X=[-\pi,-0.5\pi,0,0.5\pi,\pi] with corresponding labels y=[1,-1,-1,-1,1]. Which of the following transformations would make the data linearly separable? A. \phi(x)=(x,cos( x)) B. \phi(x)=(x,sin(x)) C. \phi(x)=(x,cos(0.5 x)) D. \phi(x)=(x,sin(0.5 x))
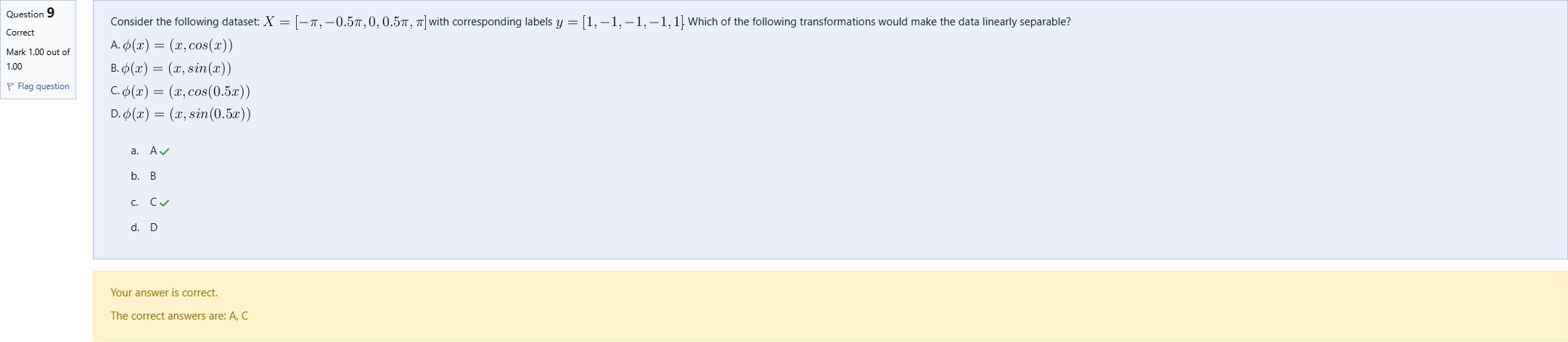
查看解析
标准答案
Please login to view
思路分析
Question restatement: Given X = [-π, -0.5π, 0, 0.5π, π] with labels y = [1, -1, -1, -1, 1], which of the following feature mappings φ(x) would make the data linearly separable?
Options:
A. φ(x) = (x, cos(x))
B. φ(x) = (x, sin(x))
C. φ(x) = (x, cos(0.5x))
D. φ(x) = (x, sin(0.5x))
Option-by-option analysis:
A) φ(x) = (x, cos(x))
- Intuition: Adding a cosine term can introduce nonlinear curvature that might separate the symmetric labels at the chosen x values. The cos(x) component oscillates between -1 and 1 with the same period as x’s domain here, which can create a decision boundary in the (x, cos x) feature space that splits the two classes more easily than in the original x-space.
- Why this could work: The first coordinate x preserves the ordering and magni......Login to view full explanation登录即可查看完整答案
我们收录了全球超50000道考试原题与详细解析,现在登录,立即获得答案。
类似问题
Let [math: x=(x1,x2)]x=(x_1,x_2) and [math: y=(y1,y2)]y=(y_1,y_2) and let kernel k be defined as follows: [math: k(x,y)=ex1x2+y1y2+2x1y1x2y2+0.25x13y13]k(x,y) = e^{x_1x_2+y_1y_2} +2 \frac{x_1 y_1}{x_2y_2} + 0.25 x_1^3 y_1^3 which transformation [math: ϕ]\phi does this kernel correspond to?
Let x=(x_1,x_2) and y=(y_1,y_2) and let kernel k be defined as follows: k(x,y) = e^{x_1x_2+y_1y_2} +2 \frac{x_1 y_1}{x_2y_2} + 0.25 x_1^3 y_1^3 which transformation \phi does this kernel correspond to?
Let [math: x=(x1,x2)]x=(x_1,x_2) and [math: y=(y1,y2)]y=(y_1,y_2) and let kernel k be defined as follows: [math: k(x,y)=ex1x2+y1y2+2x1y1x2y2+0.25x13y13]k(x,y) = e^{x_1x_2+y_1y_2} +2 \frac{x_1 y_1}{x_2y_2} + 0.25 x_1^3 y_1^3 which transformation [math: ϕ]\phi does this kernel correspond to?
Consider the following dataset: [math: X=[−π,−0.5π,0,0.5π,π]]X=[-\pi,-0.5\pi,0,0.5\pi,\pi] with corresponding labels [math: y=[1,−1,−1,−1,1]]y=[1,-1,-1,-1,1]. Which of the following transformations would make the data linearly separable? A. [math: ϕ(x)=(x,cos(x))]\phi(x)=(x,cos( x)) B. [math: ϕ(x)=(x,sin(x))]\phi(x)=(x,sin(x)) C. [math: ϕ(x)=(x,cos(0.5x))]\phi(x)=(x,cos(0.5 x)) D. [math: ϕ(x)=(x,sin(0.5x))]\phi(x)=(x,sin(0.5 x))
更多留学生实用工具
希望你的学习变得更简单
加入我们,立即解锁 海量真题 与 独家解析,让复习快人一步!