题目
多项填空题
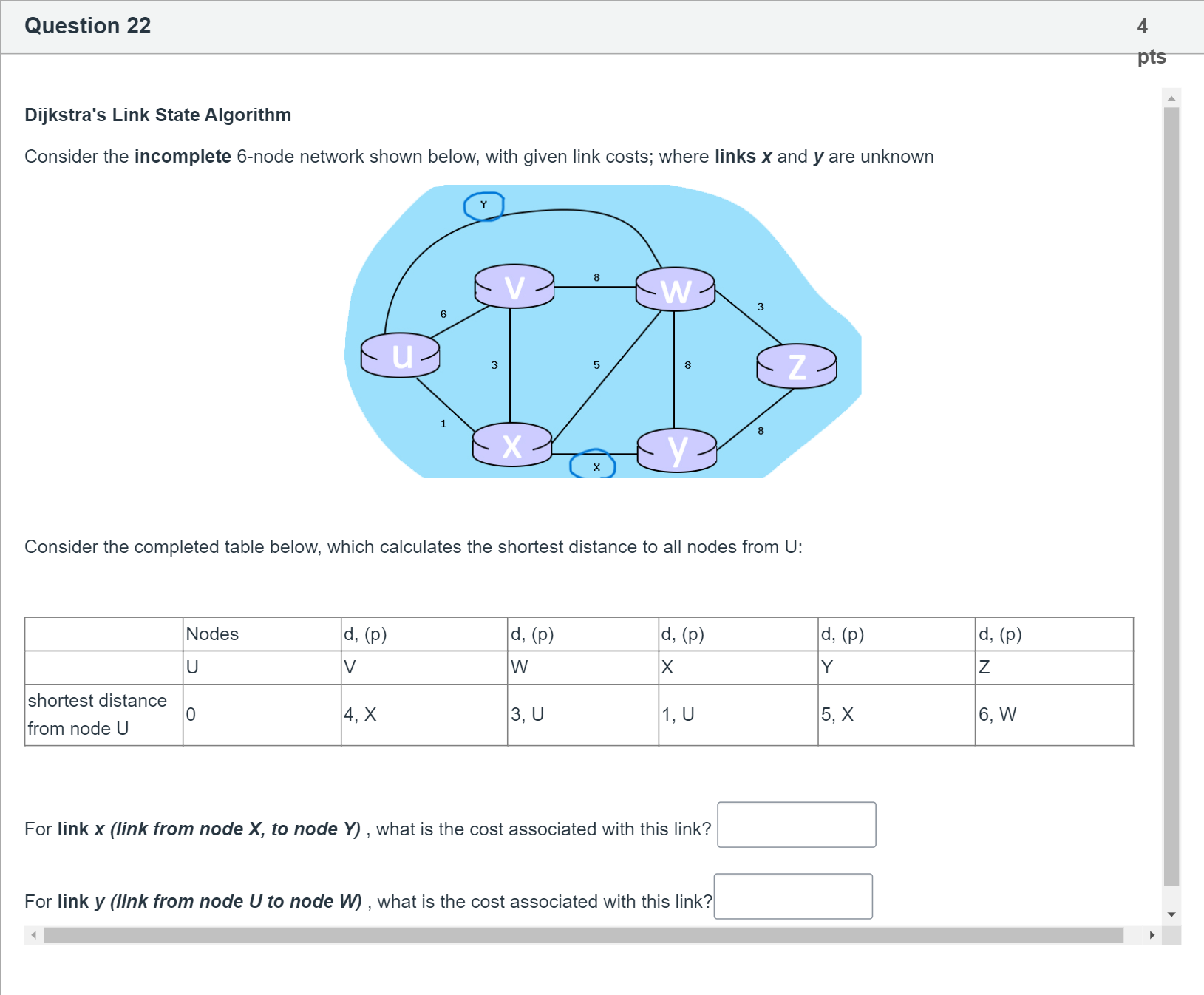
Dijkstra's Link State Algorithm Consider the incomplete 6-node network shown below, with given link costs; where links x and y are unknown Consider the completed table below, which calculates the shortest distance to all nodes from U: Nodes d, (p) d, (p) d, (p) d, (p) d, (p) U V W X Y Z shortest distance from node U 0 4, X 3, U 1, U 5, X 6, W For link x (link from node X, to node Y) , what is the cost associated with this link? [Fill in the blank] For link y (link from node U to node W) , what is the cost associated with this link?[Fill in the blank]
查看解析
标准答案
Please login to view
思路分析
First, I will restate what we are given and what we need to find, using the information embedded in the short-distance table.
The table shows the shortest distances from U to each node, along with the last node on the corresponding shortest path (in parentheses). Specifically:
- From U to V: di......Login to view full explanation登录即可查看完整答案
我们收录了全球超50000道考试原题与详细解析,现在登录,立即获得答案。
类似问题
Dijkstra’s Link-State Algorithm Consider the following network. With the indicated link costs, use Dijkstra’s shortest-path algorithm to compute the shortest path from x to all network nodes. Show how the algorithm works by computing the distance from x to all network nodes. Notes : When the distance is infinity, write in the abbreviation "inf". When there is a tie in node distances, please choose from left to right, i.e. the node in the left column is chosen first. For the N* node-set, for example, if the node-set contains nodes, x, y, and z, enter xyz in the blanks. For the D(.),p(.) column, enter in the format of "Distance, Predecessor", for example, 5,u in the blanks. Compute the distance from x to all network nodes. Step N’ D(t),p(t) D(u),p(u) D(v),p(v) D(w),p(w) D(y),p(y) D(z),p(z) 0 [Fill in the blank] [Fill in the blank] [Fill in the blank] [Fill in the blank] [Fill in the blank] [Fill in the blank] [Fill in the blank] 1 [Fill in the blank] [Fill in the blank] [Fill in the blank] [Fill in the blank] [Fill in the blank] [Fill in the blank] 2 [Fill in the blank] [Fill in the blank] [Fill in the blank] [Fill in the blank] [Fill in the blank] 3 [Fill in the blank] [Fill in the blank] [Fill in the blank] [Fill in the blank] 4 [Fill in the blank] [Fill in the blank] [Fill in the blank] 5 [Fill in the blank] [Fill in the blank] 6 [Fill in the blank] End of Table
Question at position 4 Which route computation algorithm is used by the OSPF routing mechanism?DijkstraBellman-FordNone of ThemDSR
If Dijkstra's algorithm is performed on the graph with vertex set { 0 , 1 , 2 , 3 , 4 , 5 } and adjacency matrix given below, what is the sequence of edges added to the result (shortest path tree). Use vertex 0 as a source. We break ties between vertices by picking the vertex with lower index. For example, EXTRACT-MIN returns vertex 1 before vertex 2, if both vertices have the same minimum estimate. ( 0 8 5 9 6 3 8 0 2 2 5 2 5 2 0 3 1 7 9 2 3 0 1 9 6 5 1 1 0 9 3 2 7 9 9 0 )
SPath_Alg_1 This question relates to the use of the Graph Abstract Data Type (ADT) implemented with an Adjacency Map, as covered in class. Below is the pseudocode for Dijkstra’s Algorithm: function DijkstraShortestPaths(Graph G, Vertex src): Initialize distance map d ← empty map Initialize visited set cloud ← empty set Initialize priority queue pq Initialize pqLocator ← empty map for each vertex v in G: if v == src: d[v] ← 0 else: d[v] ← ∞ pqLocator[v] ← pq.insert(d[v], v) while pq is not empty: (minDist, u) ← pq.remove_min() cloud[u] ← minDist remove pqLocator[u] for each edge (u, v) incident from u: if v not in cloud: weight ← weight of edge (u, v) if d[u] + weight < d[v]: d[v] ← d[u] + weight pq.update(pqLocator[v], d[v], v) return cloud During the execution of the while loop, under what condition does the algorithm update a vertex v’s distance and modify its position in the priority queue? Graph ADT For reference: class Vertex: def __init__(self, x): self._element = x class Edge: def __init__(self, u, v, x): self._origin = u self._destination = v self._element = x def opposite(self, v): return self._destination if v == self._origin else self._origin class Graph: def __init__(self, directed=False): self._outgoing = {} self._incoming = {} if directed else self._outgoing def incident_edges(self, v): return self._outgoing[v].values()
更多留学生实用工具
希望你的学习变得更简单
加入我们,立即解锁 海量真题 与 独家解析,让复习快人一步!