题目
MTH1030 -1035 - S1 2025 (Mission critical) Mock final exam (sample multiple choice and short answer questions)
多项填空题
Question textThis is one of the problem sets that was part of the mock exam during COVID when the exam was fully online. There will be a problem set dedicated to differential equations on the real exam. However, that one will be hand-written. In general, to prepare for the differential equation part of the final exam, please make sure that you are familiar with the sample problems in the lecture notes and the applied class problem set.a) The differential equation with the initial condition y' = 2 x y, y(0) = 2has a solution of the form y(x) =What are c and d?Answer:c= Answer 1 Question 10[input]d= Answer 2 Question 10[input]b) A possible integrating factor for this differential equation y' + 3y/x = ex/x3is xc.What is c?Answer:c= Answer 3 Question 10[input]c) The differential equation y'' + 3 y' + 3 y = 6x+21has a particular solution of the form yp(x)=ax+b. What are a and b?Answer:a = Answer 4 Question 10[input]b = Answer 5 Question 10[input]
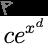
查看解析
标准答案
Please login to view
思路分析
Before diving into conclusions, let's unpack each subpart and walk through the reasoning step by step.
Part a) The differential equation y' = 2 x y with initial condition y(0) = 2.
- Approach: This is a separable first-order ODE. Rewrite as dy/y = 2x dx and integrate to obtain ln|y| = x^2 + C, so y = C e^{x^2}.
- Determining the constant: Apply the initial condition y(0) = 2, which gives 2 = C e^{0} = C. Therefore, C = 2, and the solution is y(x) = 2 e^{x^2}.
- If the problem expresses the solution in a form like y(x) = c e^{x^2} (with an extra parameter d present in the template), then c would be 2.......Login to view full explanation登录即可查看完整答案
我们收录了全球超50000道考试原题与详细解析,现在登录,立即获得答案。
类似问题
A cylindrical tank has a base radius of 5 cm and a height of 9 cm and is initially filled with water. The water flows out through a hole in the bottom of the tank at a rate of 5\( \sqrt[]{h} \)cm3/min, where h cm is the height of the water in the tank at time t. The time taken in minutes for the tank to empty is given by:
Question text 2Marks Let [math: y] be the solution to the initial value problem [math: x2dydx=ey and y(e)=1.]x^2\frac{dy}{dx}=e^{y}\ \text{ and }\ y(e)=1. Then the graph of [math: y] has an asymptote at [math: x=]Answer 5[input] and [math: y(1)=]Answer 6[input].Notes Report question issue Question 38 Notes
Consider the differential equation: . If the general solution is , which one of the following is the value of ?
The rate of consumption of a particular good is given by the differential equation 𝑑 𝑄 𝑑 𝑡 = 1560 𝑒 0.012 𝑡 . We know that Q(0)=0, that is Q=0 when t=0. Find Q(10) Note 1: There is an error margin of 5 in this question. That is, if the answer is 112.24, then any number in the interval [107.24, 117.24] will be accepted as correct. Note 2: Note: Just write the number in the space provided below. For example, if Q(10)= 6.6, then just write: 6.6
更多留学生实用工具
希望你的学习变得更简单
加入我们,立即解锁 海量真题 与 独家解析,让复习快人一步!