Questions
MAT137Y1 LEC 20249: Calculus with Proofs (all lecture sections) Pre-Class Quiz 49 (10.2)
Single choice
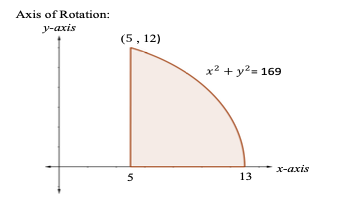
Let S be the solid of revolution obtained by rotating the shaded region in the figure below about the line y=-1. This region is bounded by x=5, y=0 and the curve 𝑥 2 + 𝑦 2 = 169 . Which two of the following definite integrals give the volume of S? I. ∫ 0 12 2 𝜋 ( 𝑦 + 1 ) 169 − 𝑦 2 𝑑 𝑦 II. ∫ 0 12 2 𝜋 𝑦 ( 169 − 𝑦 2 − 5 ) 𝑑 𝑦 III. ∫ 5 13 𝜋 ( 2 169 − 𝑥 2 + 169 − 𝑥 2 ) 𝑑 𝑥 IV. 𝜋 ∫ 5 13 ( 169 − 𝑥 2 + 1 ) 2 𝑑 𝑥 V. ∫ 0 12 2 𝜋 ( 𝑦 + 1 ) ( 169 − 𝑦 2 − 5 ) 𝑑 𝑦
Options
A.I and IV
B.II and V
C.III and V
D.II and IV
E.I and III
View Explanation
Verified Answer
Please login to view
Step-by-Step Analysis
We start by restating the scenario and listing the given options to keep the analysis clear.
Question restated: The region shaded is bounded by x = 5, y = 0, and the circle x^2 + y^2 = 169. The solid S is formed by rotating this region about the horizontal line y = -1. We are asked which two definite integrals among I–V compute the volume of S.
Answer options:
I. ∫_0^{12} 2π (y + 1) (169 − y^2) dy
II. ∫_0^{12} 2π y (169 − y^2 − 5) dy
III. ∫_5^{13} π [ (2(169 − x^2) + (169 − x^2) ) ] dx
IV. π ∫_5^{13} (169 − x^2 + 1)^2 dx
V. ∫_0^{12} 2π (y + 1) (169 − y^2 − 5) dy
To analyze, pick a suitable method. The region is better handled with horizontal slices (constant y) because the axis of rotation is horizontal (y = -1). For a slice at a fixed y, the radius of rotation is the distance from y to -1, which is y + 1. The slice’s horizontal extent runs from x = 5 ......Login to view full explanationLog in for full answers
We've collected over 50,000 authentic exam questions and detailed explanations from around the globe. Log in now and get instant access to the answers!
Similar Questions
The area bounded by the curve \( y=2sin(2x) \), the y-axis and the line y = 2 is rotated about the x-axis. The volume formed is equal to:
The area bounded by the curve y=2sin(2x)[math] y=2sin(2x) , the y-axis and the line y = 2 is rotated about the x-axis. The volume formed is equal to:
Question textThe volume of the solid of revolution formed by rotating the curve \(y=\text{Arcsin}(\frac{x}{2}), 0\leq x\leq 2\) about the \(y\)-axis is Answer 1 Question 34[input]\(\pi^2\).
Question textThe volume generated by rotating, about the \(X\) axis, the region enclosed by \(y=x^{\frac{3}{2}}\), \(x=1,x=2\), and the \(X\) axis, is Answer 1 Question 5[input] \(\pi \big/\) Answer 2 Question 5[input].
More Practical Tools for Students Powered by AI Study Helper
Making Your Study Simpler
Join us and instantly unlock extensive past papers & exclusive solutions to get a head start on your studies!