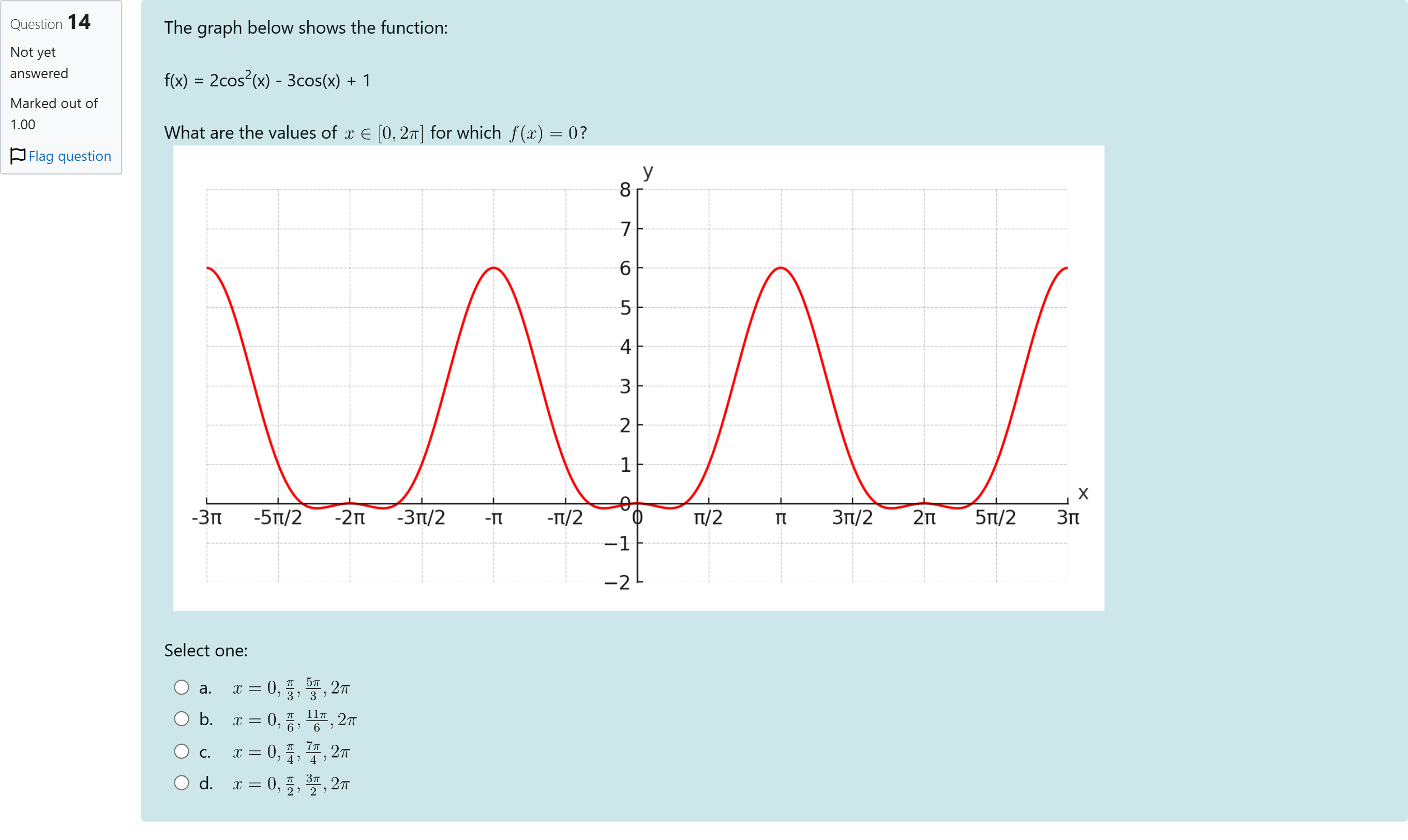
The graph below shows the function:f(x) = 2cos2(x) - 3cos(x) + 1 What are the values of for which ?

Question

BlackTom AI · Accepted Answer

We start by restating the problem: Find the values of x in [0, 2π] for which f(x) = 2cos^2(x) - 3cos(x) + 1 = 0.

First, substitute t = cos(x) to turn it into a quadratic in t: 2t^2 - 3t + 1 = 0.
Solve the quadratic by factoring: 2t^2 - 3t + 1 = (2t - 1)(t - 1) = 0, so the roots are t = 1 or t = 1/2.

Next, translate back to x values using cos(x) = t.
- If cos(x) = 1, then x = 0 or x = 2π in the interval [0, 2π].
- If cos(x) = 1/2, then x = π/3 or x = 5π/3 in [0, 2π].

Therefore the complete solution set in the interval [0, 2π] is {0, π/3, 5π/3, 2π}.

Now, evaluate each answer option:

Option a: x = 0, π/3, 5π/3, 2π
- This set matches exactly the values we found from the cosine equations cos x = 1 and cos x = 1/2. It includes all and only the correct x-values in [0, 2π], so it is correct.

Option b: (typical incorrect reasoning) This option likely omits some of the correct x-values or includes extraneous ones. For example, if it misses 0 or 2π, it’s incomplete; if it includes an angle where cos x is not 1 or 1/2, it’s incorrect because it would not satisfy f(x) = 0.

Option c: (typical incorrect reasoning) This option might present only the cos x = 1/2 solutions (π/3 and 5π/3) or only the cos x = 1 solutions (0 and 2π) or introduce angles outside [0, 2π]. Any deviation from the full set {0, π/3, 5π/3, 2π} fails to capture all zeros of f on the given interval.

Option d: (typical incorrect reasoning) This option could include angles that correspond to cos x values not equal to 1 or 1/2, or it could reorder them without changing the set. If it contains any extra angles beyond the valid ones, or misses some, it’s incorrect.

In summary, the correct logic is factoring the quadratic in cos x, solving for cos x, mapping back to x in [0, 2π], which yields exactly the four angles 0, π/3, 5π/3, and 2π. All other options fail to reproduce this complete and precise set, either by omitting a valid value, including an invalid one, or both.

MHF4U - Advanced Functions 12 (2025-26) - A

The graph below shows the function:f(x) = 2cos2(x) - 3cos(x) + 1 What are the values of for which ?

查看解析

登录即可查看完整答案

类似问题

Solve the equation:2cos(x) +1 = 0for all values of . Select the correct set of solutions.

Question textSolve the equation [math: 3tan⁡(x)−3=0]{3\,\tan \left( x \right)-\sqrt{3}=0} over [math: [0,2π]]\displaystyle \Big[0, 2\pi \Big] in radians. Note. Type pi to enter [math: π]\pi and use { , } to enter a set.[input] Check Question 4

Question textSolve the equation [math: tan⁡(x)−3=0]{\tan \left( x \right)-\sqrt{3}=0} over [math: [0,2π]]\displaystyle \Big[0, 2\pi \Big] in radians. Note. Type pi to enter [math: π]\pi and use { , } to enter a set.[input] Check Question 4

更多留学生实用工具

考试浏览器助手

风格化写作助手

论文查重助手

文献引用助手

课堂转译助手

课堂笔记助手

Quiz搜索助手

学校历年真题

智能刷题助手

智能匹配练习

希望你的学习变得更简单