Still overwhelmed by exam stress? You've come to the right place!
We know exam season has you totally swamped. To support your studies, access Gold Membership for FREE until December 31, 2025! Normally £29.99/month. Just Log In to activate – no strings attached.
Let us help you ace your exams efficiently!
Questions
ANATOMY 2300 AU2025 (34636) Practice Quiz for Unit Exams- Requires Respondus LockDown Browser
Single choice
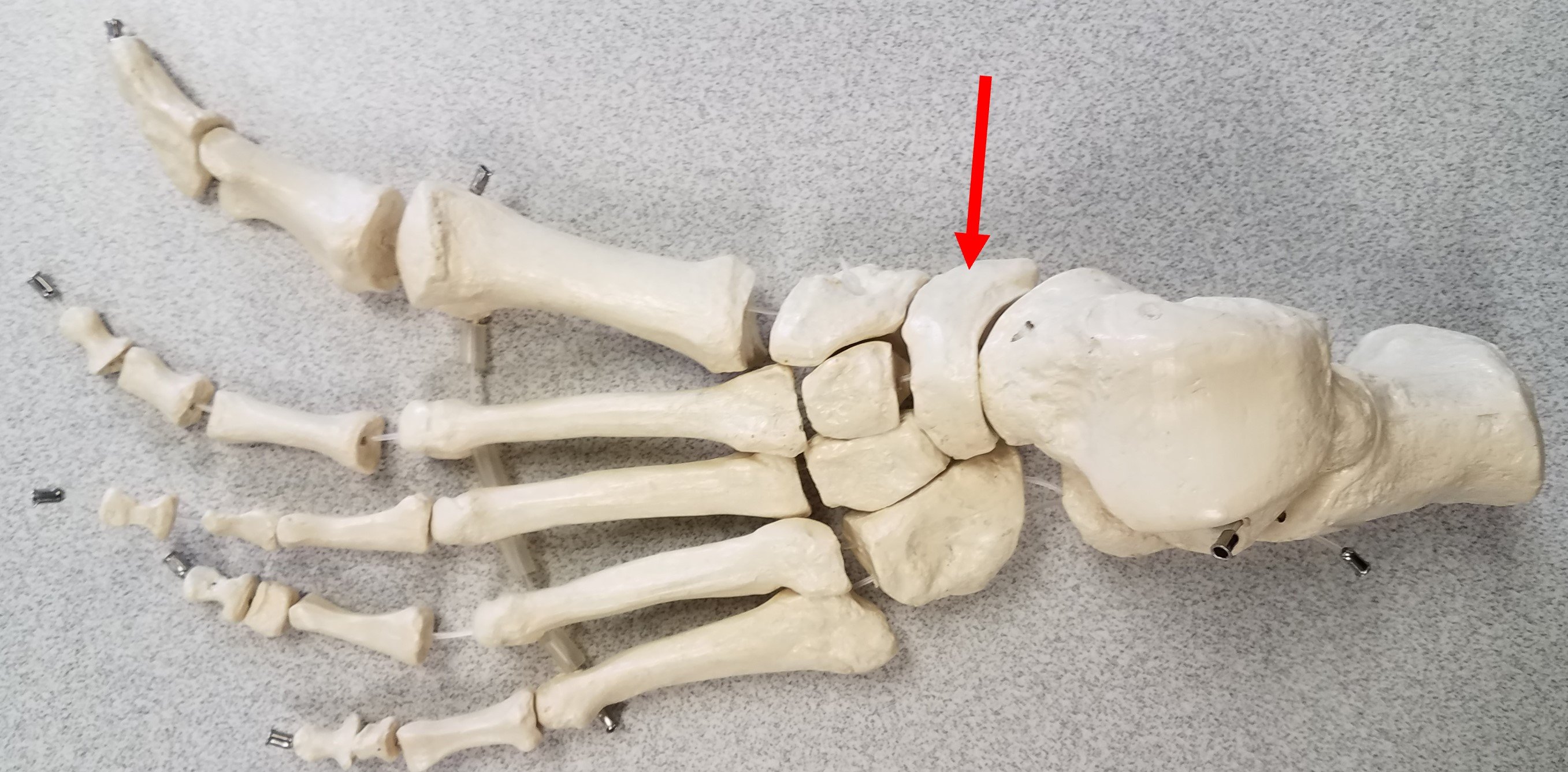
Identify the bone indicated by the arrow in the image below.
Options
A.Navicular
B.Medial cuneiform
C.Cuboid
D.Calcaneus
E.Talus
View Explanation
Standard Answer
Please login to view
Approach Analysis
Question: Identify the bone indicated by the arrow.
Option 1: Navicular — This is the bone in the midfoot on the medial side, articulating with the talus posteriorly and the three cuneiforms anteriorly. The arrow points to a bone located between the t......Login to view full explanationLog in for full answers
We've collected over 50,000 authentic exam questions and detailed explanations from around the globe. Log in now and get instant access to the answers!
Similar Questions
Question at position 1 Which tarsal bone articulates with the tibia and fibula?talusnavicularcalcaneuscuboid
Superior view The tarsal bone labelled A is the __ [ Select ] 1st (medial) cuneiform bone navicular cuboid talus calcaneus __. The joint indicated by label B is the __ [ Select ] tarsometatarsal metatarsophalangeal interphalangeal intertarsal __ joint, this is a __ [ Select ] gliding hinge condyloid pivot ball and socket ___ joint.
Question text The students below each construct a sinusoidal function based on a shared scenario involving water level fluctuations.Match each student’s reasoning to the explanation that best fits their thinking. Scenario:The depth of water , in metres, at a canal dock fluctuates due to the system of canal locks lowering and raising the water for container ships. The water varies sinusoidally from a minimum of 1.5 m to a maximum of 4.5 m. The depth reaches its minimum at 5:00 AM, and one full cycle of the water level is completed every 4 hours. The horizontal axis represents time , in hours, where corresponds to midnight. Student 1:I was asked to find the water depth at 3 AM.The equation I created was Since the minimum occurs at 5:00 AM, I shifted the function by 5.Using this function, I found the depth at 3 AM was 1.5 m.Answer 1 Question 22[select: , All parameters are correct. Therefore, the initial evaluation is correct, and the correct depth at 3 AM is 1.5 m. , All parameters are correct except the phase shift: there should be a phase shift of -5. Therefore, the initial evaluation is incorrect; using the new equation, the correct depth at 3 AM is 4.5 m. , All parameters are correct except the k-value: the k-value should be pi/4. The initial evaluation is still correct; the depth at 3 AM is 1.5 m.] Student 2:I was asked to find the water depth at 6 AM.The equation I created was I chose sine because the water starts rising after its lowest point.Using my equation, I found the depth at 6 AM was 3 m.Answer 2 Question 22[select: , All parameters are correct except for the amplitude, which should be negative. The initial evaluation is still correct; the depth at 6 AM is 3 m., All parameters are except the phase shift: there should be a phase shift of -5. Therefore, the initial evaluation is incorrect; using the new equation, the correct depth at 6 AM is 4.1 m., All parameters are correct except the k-value; the k-value should be pi/2. The initial evaluation is still correct; the depth at 6 AM is 3 m. ] Student 3:I was asked to find the water depth at 1 PM.The equation I created was Since the minimum occurs at 5:00 AM, I used a cosine function with a shift to match the point.I found the depth at 1 PM to be 4.5 m.Answer 3 Question 22[select: , All parameters are correct except the k-value; the correct k-value is pi/4. The initial evaluation is still correct; the depth at 1 PM is 4.5 m., All parameters are correct except for the phase shift; there should be a phase shift of -3. Therefore, the initial evaluation is incorrect; using the new equation, the correct depth at 1 PM is 1.5 m.. , All parameters are correct and the student’s evaluation of the depth was correct; the depth at 1 PM is 4.5 m.]
The point lies on the terminal arm of an angle in standard position. What are the correct values of the following three ratios?
More Practical Tools for International Students
Making Your Study Simpler
To make preparation and study season easier for more international students, we've decided to open up Gold Membership for a limited-time free trial until December 31, 2025!