Still overwhelmed by exam stress? You've come to the right place!
We know exam season has you totally swamped. To support your studies, access Gold Membership for FREE until December 31, 2025! Normally £29.99/month. Just Log In to activate – no strings attached.
Let us help you ace your exams efficiently!
Questions
Dashboard ENG2081: Mechanics of Structures 2A (2025-26)
Numerical
If the second moment of area for the I-section ( [math: Izz] I_{zz} ) shown below is 39848803 mm4, determine the breadth of the flange, b, in mm, (to 1 decimal place) given the following: d=169 mm, w=11 mm and t=16 mm.
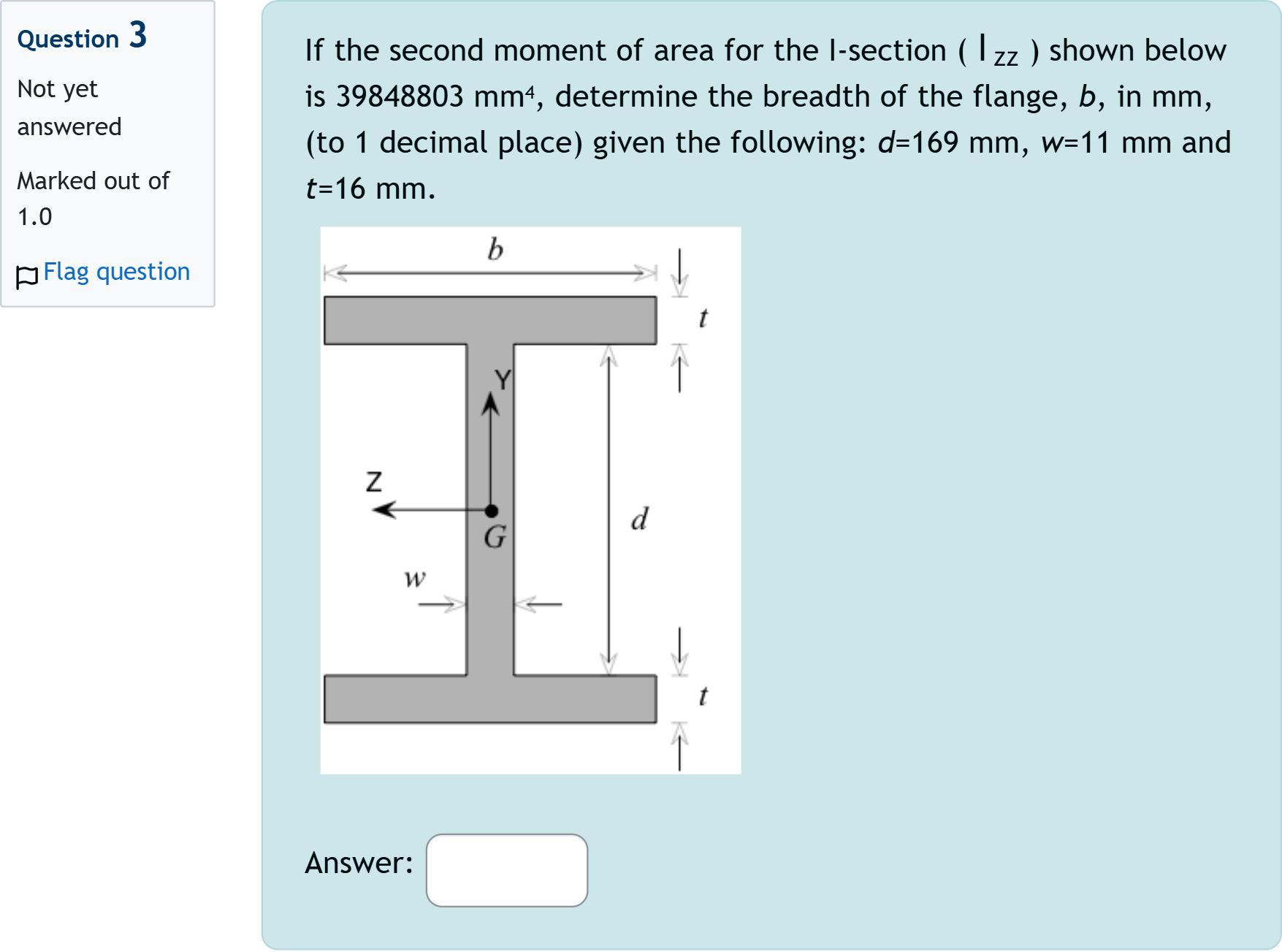
View Explanation
Standard Answer
Please login to view
Approach Analysis
We are given an I-section with flange width b, flange thickness t, web width w, overall depth d, and the required second moment of area about the zz axis, Izz = 39 848 803 mm^4. The cross-section consists of two identical flanges (top and bottom) connected by a web. To relate Izz to the geometric dimensions, we sum the contributions of each simple rectangle (two flanges and the web) about the centroidal zz axis and use the parallel-axis theorem where appropriate.
Step 1: Identify the individual pieces and their centroids.
- Top flange: width b, thickness t. Its own centroid lies t/2 above the top surface. Its distance from......Login to view full explanationLog in for full answers
We've collected over 50,000 authentic exam questions and detailed explanations from around the globe. Log in now and get instant access to the answers!
Similar Questions
The section has a length and height of [math: b] = 0.48 m, and the circular hole has a diameter of [math: D] = 0.1 m. Given that the centroid [math: G] is exactly at the center of the geometry, calculate the second moment of area about the z axis [math: Izz] I_{zz} . For this question, take [math: π]\pi = 3.14. The second moment of area for a circle is [math: I=πD464] I=\frac{\pi{D^4}}{64} . Provide the answer in [math: mm4] mm^4 , rounded to a decimal place.
Which of these expressions is correct regarding the relative sizes of cracked, gross and effective second moment of inertia?
The centroid location of the shape shown is 91.67 mm, measured from the bottom of the part. What is the moment-of-inertia of the shape about the centroidal x-axis?
This question continues previous question 32. Based on the cost information provided in Question 32 and a Weighted Average Contribution Margin (WACM) of 160 per unit calculate the break-even point in units for Model A. Note: Round to full numbers, provide your answer without the unit sign, i.e., X,XXX, and show your workings. Answer: [Fill in the blank] , Working space: [Fill in the blank]
More Practical Tools for International Students
Making Your Study Simpler
To make preparation and study season easier for more international students, we've decided to open up Gold Membership for a limited-time free trial until December 31, 2025!