Questions
FNDN 2025 O1 Challenge Week 2 Examinations
Single choice
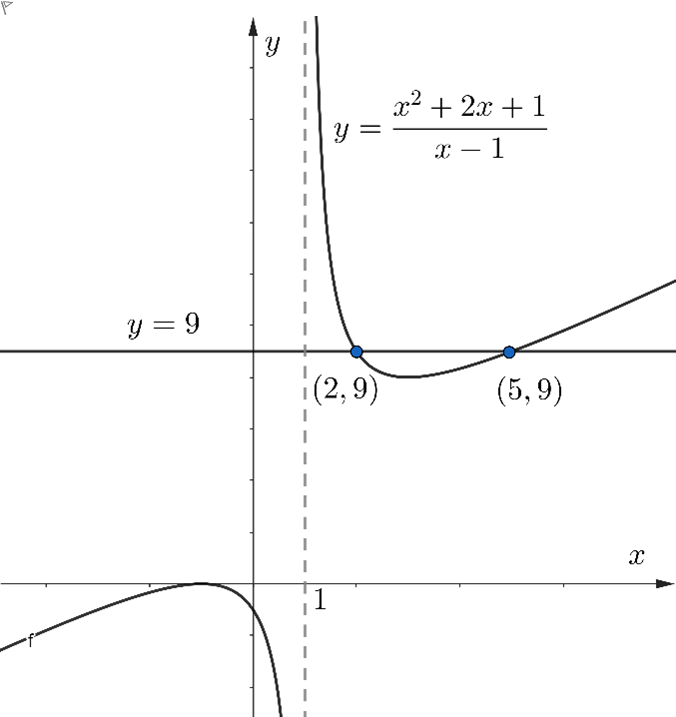
The graphs of the line [math: y=9] and the curve [math: y=x2+2x+1x−1]y=\dfrac{x^2+2x+1}{x-1} intersect at the points [math: (2,9)](2, 9) and [math: (5,9)](5, 9) , as shown in the diagram below. State the solution to the inequality [math: x2+2x+1x−1≤9]\dfrac{x^2+2x+1}{x-1}\leq 9 .
Options
A.[math: 2≤x≤5]2 \leq x \leq 5
B.[math: 1<x≤2 or x≥5]1\lt x \leq 2 \text{ or } x\geq 5
C.[math: x<1]x \lt 1
D.[math: x<1 or 2≤x≤5]x\lt 1 \text{ or } 2 \leq x\leq 5
View Explanation
Verified Answer
Please login to view
Step-by-Step Analysis
We begin by translating the given inequality into a rational inequality that we can analyze piece by piece.
Option analysis often hinges on identifying critical points where the expression changes sign or becomes undefined.
First, rewrite the expression: y = (x^2 + 2x + 1)/(x - 1) ≤ 9. Notice the numerator factors as (x + 1)^2, so we have (x + 1)^2/(x - 1) ≤ 9.
To bring everything to one side, subtract 9 from both sides: (x + 1)^2/(x - 1) - 9 ≤ 0. Get a common denominator to combine: [(x + 1)^2 - 9(x - 1)]/(x - 1) ≤ 0.
Expanding the numerator yields (x^2 + 2x + 1) - 9x + 9 = x^2 - 7x + 10,......Login to view full explanationLog in for full answers
We've collected over 50,000 authentic exam questions and detailed explanations from around the globe. Log in now and get instant access to the answers!
Similar Questions
Question textThe students below solved rational inequalities. Match each student’s reasoning to the best explanation.Student 1:“I solved \frac{1}{x+1} < 5 and wrote the solution intervals as x < -1 or x > -\frac{4}{5} .” Answer 1 Question 22[select: , The student found the correct critical points but only x < -1 is a valid interval; x > -4/5 is not valid., The student listed the correct critical points but mistakenly concluded the interval solution; the correct solution is -1 < x < -4/5., The student correctly solved the inequality and gave appropriate solution intervals using the correct critical points.]Student 2:“I solved \frac{2x}{x-1} > 3 and wrote x > 3 as my solution interval.” Answer 2 Question 22[select: , The student correctly identified the critical points and the solution; the correct interval is x > 3., The student identified the correct critical points, but the solution is incorrect; the correct solution is x < 1, x > 3., The student identified the correct critical points but the solution is incorrect; the correct solution is 1 < x < 3. ]Student 3:“I solved \frac{x+4}{x-3} < 2 and listed critical points at x = -4 and x = 3 .” Answer 3 Question 22[select: , The student correctly listed the critical values as x = -4 and x = 3., The student attempted to identify critical points but incorrectly listed x = -4; the correct critical points are x = 3 and x = 10., The student attempted to identify critical points but incorrectly listed x = -4 instead of x = 2; the correct critical points are x = 3 and x = 2.]
Which of the following intervals are part of the solution set of x 2 − 3 x − 4 x 2 − x − 2 ≥ 0 ? {"version":"1.1","math":"\dfrac{x^2-3x-4}{x^2-x-2}\ge 0?"}
Consider the inequalities:[math: d1:(x−1)(x+3)≥0] d_1: \quad (x-1)(x+3) \ge 0 [math: d2:x−1x+3≥0] d_2: \quad \frac{x-1}{x+3} \ge 0
In a consumer society, many adults channel creativity into buying things
More Practical Tools for Students Powered by AI Study Helper
Making Your Study Simpler
Join us and instantly unlock extensive past papers & exclusive solutions to get a head start on your studies!