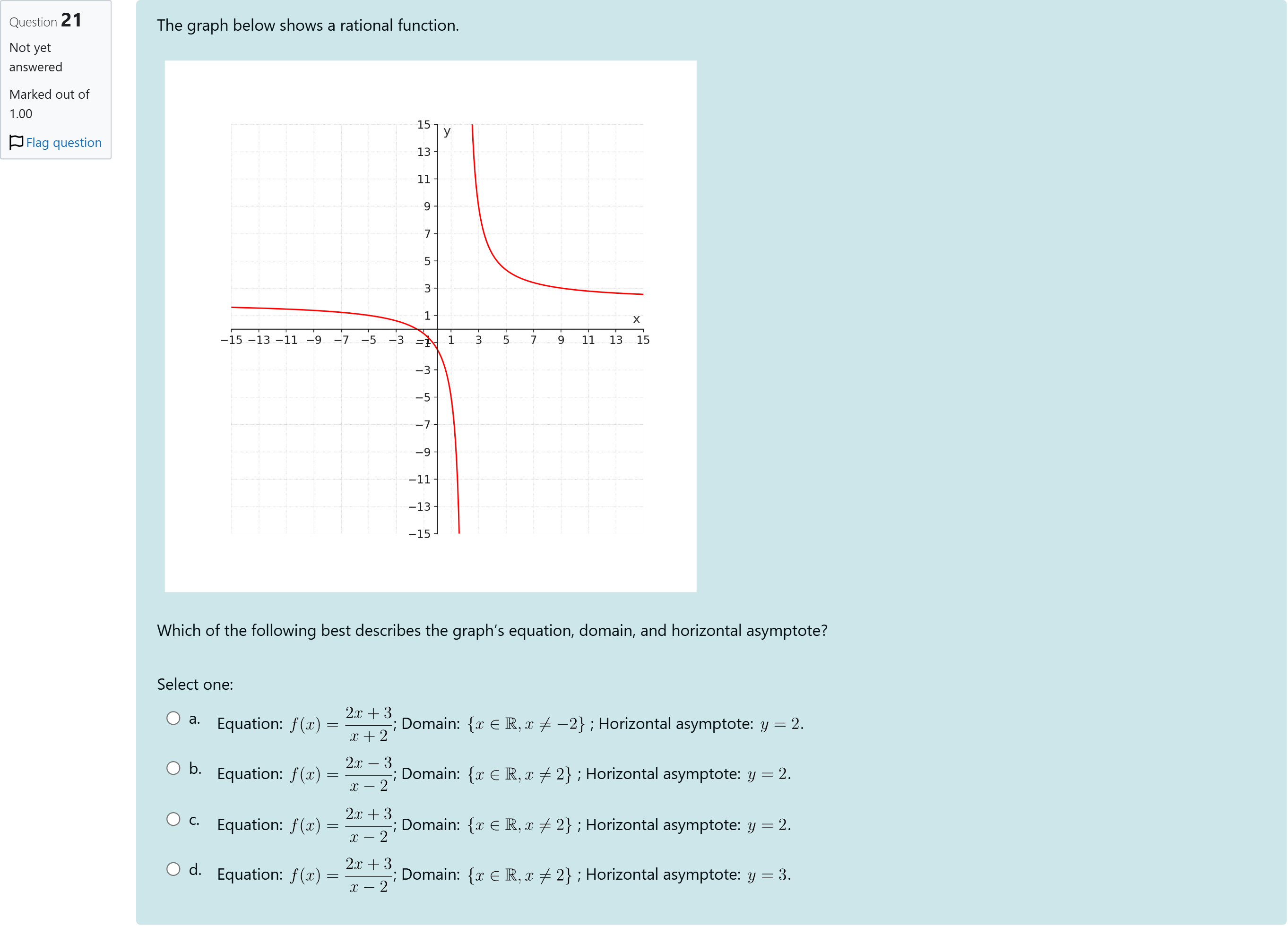
The graph below shows a rational function.Which of the following best describes the graph’s equation, domain, and horizontal asymptote?

Question

BlackTom AI · Accepted Answer

Let me restate the problem and all answer choices to begin.
Question: The graph below shows a rational function. Which of the following best describes the graph’s equation, domain, and horizontal asymptote?
Answer options:
- a. Equation: f(x) = \dfrac{2x + 3}{x + 2} ; Domain: \{ x \in \mathbb{R}, x 
eq -2 \} ; Horizontal asymptote: y = 2 .
- b. Equation: f(x) = \dfrac{2x - 3}{x - 2} ; Domain: \{ x \in \mathbb{R}, x 
eq 2 \} ; Horizontal asymptote: y = 2 .
- c. Equation: f(x) = \dfrac{2x + 3}{x - 2} ; Domain: \{ x \in \mathbb{R}, x 
eq 2 \} ; Horizontal asymptote: y = 2 .
- d. Equation: f(x) = \dfrac{2x + 3}{x - 2} ; Domain: \{ x \in \mathbb{R}, x 
eq 2 \} ; Horizontal asymptote: y = 3 .

Now, I will analyze each option in turn, explaining what each component means and whether it matches the graph’s features.

Option a:
- The equation is f(x) = (2x + 3)/(x + 2). The numerator 2x + 3 is plausible for a linearly shaped rational function, but the denominator is x + 2 rather than x − 2. This change in the vertical line where the function is undefined (a vertical asymptote) would occur at x = −2, not x = 2. If the graph shows a vertical asymptote at x = 2, this option would be incorrect. 
- The domain claim is { x ∈ R, x ≠ −2 }, which aligns with a vertical asymptote at x = −2. If the graph indeed has an asymptote at x = 2 instead, this is a mismatch.
- The horizontal asymptote is given as y = 2. For a rational function where degrees of numerator and denominator are equal, the horizontal asymptote is the ratio of leading coefficients, which here would be 2/1 = 2. So the HA being y = 2 could be correct, but only if the other parts align.
Overall, because the denominator in this option is x + 2, which implies a vertical asymptote at x = −2, this would be inconsistent with a typical graph showing a vertical asymptote at x = 2. If the graph shows x = 2 as the vertical asymptote, option a is incorrect.

Option b:
- The equation is f(x) = (2x − 3)/(x − 2). Here the denominator x − 2 indicates a vertical asymptote at x = 2, which matches a common right-hand vertical asymptote location. The numerator is 2x − 3, which changes the y-intercept and the overall shape compared to 2x + 3. 
- The domain { x ∈ R, x ≠ 2 } correctly reflects the vertical asymptote at x = 2. If the graph shows a singularity at x = 2, this part is consistent.
- The horizontal asymptote is y = 2. Since the degrees are equal and the leading coefficients are 2 (numerator) and 1 (denominator), the HA is y = 2/1 = 2, which matches.
So all three components could be consistent with a graph that has a vertical asymptote at x = 2 and HA y = 2, provided the numerator’s exact value aligns with the graph’s crossing or intercepts. If the graph’s intercepts or curvature correspond to 2x − 3 rather than 2x + 3, this option could still be plausible.

Option c:
- The equation is f(x) = (2x + 3)/(x − 2). This has numerator 2x + 3 and denominator x − 2, yielding a vertical asymptote at x = 2, which is a common placement for a rational function’s pole. The numerator aligns with a line that would pass through a certain y-intercept and slope; the combination with the denominator determines the graph’s stretch and shift.
- The domain { x ∈ R, x ≠ 2 } again correctly excludes the vertical asymptote at x = 2.
- The horizontal asymptote y = 2 follows from the leading terms: 2x/ x = 2 as x → ±∞, so HA = 2 is correct for this ratio of leading coefficients.
If the graph indeed shows a vertical asymptote at x = 2 and a horizontal asymptote at y = 2, and the intercept behavior matches a numerator of 2x + 3, this option would be consistent.

Option d:
- The equation f(x) = (2x + 3)/(x − 2) has the same algebraic form as option c, so the vertical asymptote is at x = 2 and the domain excludes x = 2, which is consistent with a pole there.
- The horizontal asymptote is listed as y = 3 in this option. However, for a rational function where the degrees of numerator and denominator are equal, the horizontal asymptote is the ratio of leading coefficients, which would be 2/1 = 2, not 3. This makes the HA in this option incorrect given the standard rule for horizontal asymptotes of proportionally leading terms.
- Since the HA is incorrect, option d is inconsistent with the standard end-behavior of this rational function form.

Summary of the reasoning approach:
- Check the vertical asymptote location by inspecting the denominator. If the graph shows a vertical asymptote at x = 2, options with x − 2 in the denominator are possible; those with x + 2 would place the asymptote at x = −2 and would be incorrect for a graph showing x = 2 as the vertical asymptote.
- Check the horizontal asymptote by comparing the degrees of the numerator and denominator and the leading coefficients. If the degrees are equal, HA = ratio of leading coefficients. Here, with leading coefficients 2 (numerator) and 1 (denominator), HA = 2. Any option claiming HA = 3 would be incorrect.
- Check the domain. If the graph has a hole or a vertical asymptote, the domain excludes the corresponding x-values. The stated domain should reflect the same exclusion, i.e., x ≠ 2 for a vertical asymptote at x = 2.

Keeping all these criteria in mind, you can compare each option to the features suggested by the graph. Note how small changes in the numerator or the denominator alter either intercepts, the vertical asymptote location, or the horizontal asymptote, which in turn discriminates between options.

MHF4U - Advanced Functions 12 (2025-26) - A

The graph below shows a rational function.Which of the following best describes the graph’s equation, domain, and horizontal asymptote?

View Explanation

Log in for full answers

Similar Questions

Find the [math: y] intercept of [math: f(x)=4x2+36x+3+−7] f(x)= \frac{4x^2+3}{6x+3} +-7 Give your answer correct to 2 decimal places.

Computing Rational Functions For the given functions and , do the following computation. Choose the best answer. and Find

Computing Rational Functions For the given functions f(x) and g(x), do the following computation. Choose the best answer. f(x)= 5x+1 8x−1 and g(x)= 3x 8x−1 Find f g (x)

Computing Rational Functions For the given functions 𝑓 ( 𝑥 ) and 𝑔 ( 𝑥 ) , do the following computation. Choose the best answer. 𝑓 ( 𝑥 ) = 5 𝑥 + 1 8 𝑥 − 1 and 𝑔 ( 𝑥 ) = 3 𝑥 8 𝑥 − 1 Find 𝑓 𝑔 ( 𝑥 )

Given the following features of a rational function:x-intercept: -2 y-intercept: -3 vertical asymptote: x = 2horizontal asymptote: y = 3 Which of the following is the correct equation?

For which interval is f(x) = \dfrac{1}{x - 2} negative?

The range of 𝑦 = 9 7 − 𝑥

Choose which graph best represents the curve [math: y=4−1x−2]y=4 - \dfrac{1}{x-2} .

More Practical Tools for Students Powered by AI Study Helper

Homework AI Solver

Stylized AI Paper Writer

Plagiarism Checker Assistant

Citation AI Academic Writing Tool

In-Class Translation Assistant

AI Note Generator

AI Quiz Answers

Past Exam Questions from University Test Bank

Smart Practice Assistant

Adaptive Practice

Making Your Study Simpler