Questions
COMP 543 001 Quiz 4
Single choice
In class, I asserted that is the same as , where and are predicates. That is, you can "not" or "negate" a predicate that is itself a conjunction of predicates by distributing the "not" over the inner predicates, and changing the "and" to an "or". Using this rule, and the fact that is equivalent to and also that is equivalent to , we can argue that can be re-written as what?
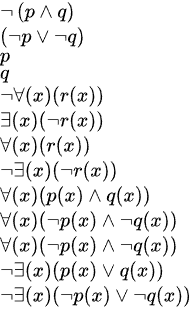
View Explanation
Verified Answer
Please login to view
Step-by-Step Analysis
The prompt asks us to rewrite the negation of a conjunction of predicates using the given logical equivalences, but the provided data has no answer options to analyze. I will nevertheless walk through the correct transformation and point out common missteps that might appear.
First, recall De Morgan’s law for predicates: not (A and B) is equivalent to (not A) or (not B). When the domain involves a ......Login to view full explanationLog in for full answers
We've collected over 50,000 authentic exam questions and detailed explanations from around the globe. Log in now and get instant access to the answers!
Similar Questions
Formulate two distinct logical predicates that accurately represent the following new information: “News247 is a news application that has a rating of 8.” The predicates should follow to the previously established syntax and representation schema of the knowledge base. (6 marks)
A predicate can be described as… (Pick the statement that applies.)
Which of the following is not an example of a predicate?
Suppose isPositive(X) evaluates to True when X is a positive number, and False otherwise. If X = -2, which of the following is not true about isPositive(X)?
More Practical Tools for Students Powered by AI Study Helper
Making Your Study Simpler
Join us and instantly unlock extensive past papers & exclusive solutions to get a head start on your studies!