Questions
Questions
Numerical

Compute the partial derivative of f(x,y,\lambda)=2x+y+\lambda(x^2+y^2-2.9) with respect to \lambda at point (x,y,\lambda)=(1,2,0).

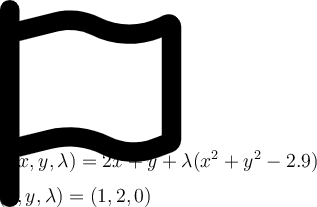
Question Image
View Explanation

View Explanation

Verified Answer
Please login to view
Step-by-Step Analysis
To find the partial derivative of f with respect to λ, treat x and y as constants and ......Login to view full explanation

Log in for full answers

We've collected over 50,000 authentic exam questions and detailed explanations from around the globe. Log in now and get instant access to the answers!

Similar Questions

Question at position 2 If z=yx2+6yz=y\sqrt{x^2+6y}, then ∂z∂y=\frac{\partial z}{\partial y\:}= yx2+6y+x2+6y\frac{y}{\sqrt{x^2+6y}}+\sqrt{x^2+6y}3yx2+6y\frac{3y}{\sqrt{x^2+6y}}3yx2+6y+x2+6y\frac{3y}{\sqrt{x^2+6y}}+\sqrt{x^2+6y}(2x+6)yx2+6y\left(2x+6\right)y\sqrt{x^2+6y}x2+6y\sqrt{x^2+6y}

Question at position 1 If f(x,y,z)=x2yz2+xy2z+xyf\left(x,y,z\right)=x^2yz^2+xy^2z+xy, then fx(1, 2, 3) =36.none of the above55.50.48.

Question text 6Marks Consider the function [math: f(x,y)=x2y2+yex−1.] f(x,y) = x^2y^2 +y e^{x-1} . a) Calculate the following partial derivatives at the point [math: (1,1)]: [math: ∂f∂x=]\frac{\partial f}{\partial x}= Answer 1[input] [math: ∂f∂y=]\frac{\partial f}{\partial y}= Answer 2[input] [math: ∂2f∂x2=]\frac{\partial^2 f}{\partial x^2}= Answer 3[input] [math: ∂2f∂x∂y=]\frac{\partial^2 f}{\partial x\partial y}= Answer 4[input] [math: ∂2f∂y2=]\frac{\partial^2 f}{\partial y^2}= Answer 5[input] b) A tangent vector to the level set of [math: f] at [math: (1,1)] is [math: (1,] Answer 6[input][math: )].Notes Report question issue Question 5 Notes

Question textLet [math: f(x,y)=ey+x2]f(x,y)={e^{y+x^2}}. What is [math: ∂f∂x(0,0)+∂f∂y(0,0)]\frac{\partial f}{\partial x}(0,0) + \frac{\partial f}{\partial y}(0,0), the value of [math: ∂f∂x+∂f∂y]\frac{\partial f}{\partial x} + \frac{\partial f}{\partial y} at the point [math: (0,0)] ?[input] Check Question 67

More Practical Tools for Students Powered by AI Study Helper

Join us and instantly unlock extensive past papers & exclusive solutions to get a head start on your studies!