Still overwhelmed by exam stress? You've come to the right place!

We know exam season has you totally swamped. To support your studies, access Gold Membership for FREE until December 31, 2025! Normally £29.99/month. Just Log In to activate – no strings attached.

Let us help you ace your exams efficiently!

Questions
Questions

MAT-265-OD24-02-7799

Multiple fill-in-the-blank

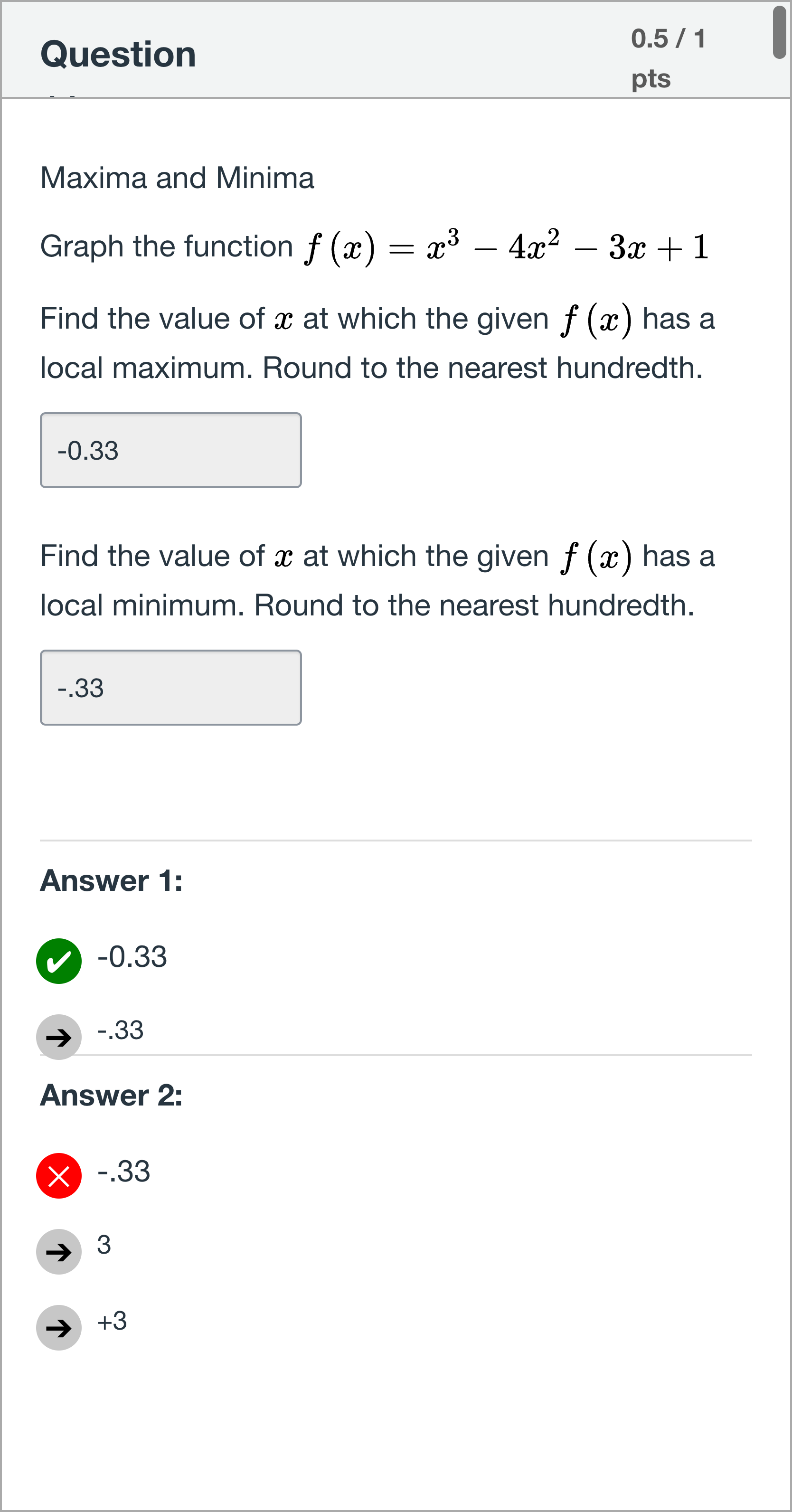
Maxima and Minima Graph the function Find the value of at which the given  has a local maximum. Round to the nearest hundredth. [Fill in the blank] Find the value of at which the given  has a local minimum. Round to the nearest hundredth. [Fill in the blank]

Question Image
View Explanation

View Explanation

Standard Answer
Please login to view
Approach Analysis
We start by identifying the critical points of the function to locate potential local maxima and minima. Option set: The problem asks for the x-values where the given f(x) = x^3 - 4x^2 - 3x + 1 has a local maximum and a local minimum. The derivative will guide us to candidate points. 1) Compute the derivative: f'(x) = d/dx [x^3 - 4x^2 - 3x + 1] = 3x^2 - 8x - 3. 2) Find critical points by solving f'(x) = 0: 3x^2 - 8x - 3 = 0. ......Login to view full explanation

Log in for full answers

We've collected over 50,000 authentic exam questions and detailed explanations from around the globe. Log in now and get instant access to the answers!

Similar Questions

Find the absolute (global) maximum \( y \) value of the function:\( f(x)=2x^3+0x^2+-24x+5 \)On the interval \( [-9, 10] \)

Find the absolute (global) maximum [math: y] value of the function:[math: f(x)=2x3+0x2+−24x+5]On the interval [math: [−9,10]]

Maxima and Minima Graph the function f(x)=x3−4x2−3x+1f\left(x\right)=x^3-4x^2-3x+1 Find the value of xx at which the given f(x)f\left(x\right) has a local maximum. Round to the nearest hundredth. [Fill in the blank] Find the value of xx at which the given f(x)f\left(x\right) has a local minimum. Round to the nearest hundredth. [Fill in the blank]

Find the extreme values of the function and where they occur. y =

More Practical Tools for International Students

To make preparation and study season easier for more international students, we've decided to open up Gold Membership for a limited-time free trial until December 31, 2025!