Questions
Questions

ETF2700 - ETF5970 - S2 2025 Quiz 2

Numerical

Define the matrices A=\left[\begin{array}{ccc} 2&3\\ {1}&{-5}\end{array}\right] and B=\left[\begin{array}{ccc} 4&3&6\\ {1}&2.8&3\end{array}\right]. What is the entry in the first row and second column of AB?

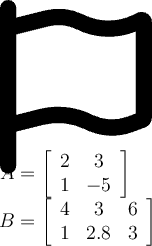
Question Image
View Explanation

View Explanation

Verified Answer
Please login to view
Step-by-Step Analysis
To find the (1,2) entry of AB, I’ll multiply the first row of A by the second column of B. First, ident......Login to view full explanation

Log in for full answers

We've collected over 50,000 authentic exam questions and detailed explanations from around the globe. Log in now and get instant access to the answers!

Similar Questions

Vector a =  10      12 And vector b =  2 3   Whats the value of a*b ?  (* is matrix multiplication);  Please enter a number with no decimals.  

Question at position 13 [1−12][[4−10][23]+[1001−11]]=\begin{bmatrix} 1 & -1 & 2 \\ \end{bmatrix} \left[ \begin{bmatrix} 4 \\ -1\\ 0 \end{bmatrix} \begin{bmatrix} 2 &3 \\ \end{bmatrix} + \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ -1 & 1 \end{bmatrix} \right] =[2−34810]\begin{bmatrix} 2 & -3 \\ 4 & 8 \\ 1 & 0 \end{bmatrix}none of the above[29−3]\begin{bmatrix} 2 & 9 & -3 \\ \end{bmatrix}[5−7]\begin{bmatrix} 5 \\ -7 \end{bmatrix}[912]\begin{bmatrix} 9 & 12 \\ \end{bmatrix}

Question at position 12 [1−134][025−3]=\begin{bmatrix} 1 & -1 \\ 3 & 4 \end{bmatrix} \begin{bmatrix} 0 & 2 \\ 5 & -3 \end{bmatrix} =[−5520−6]\begin{bmatrix} -5 & 5 \\ 20 & -6 \end{bmatrix}[68−4−17]\begin{bmatrix} 6 & 8 \\ -4 & -17 \end{bmatrix}[−2838]\begin{bmatrix} -2 & 8 \\ 3 & 8 \end{bmatrix}[4−106]\begin{bmatrix} 4 & -1 \\ 0 & 6 \end{bmatrix}[0−215−12]\begin{bmatrix} 0 & -2 \\ 15 & -12 \end{bmatrix}

Consider the matrix: \[ \mathbf {X=}\begin {pmatrix} 1 & 0 & 0 \\ 1 & 1 & 0 \\ 1 & 1 & 0 \\ 1 & 0 & 1 \end {pmatrix}.\]Which one of the following matrices is \(\mathbf {X}’\mathbf {X}\)?

More Practical Tools for Students Powered by AI Study Helper

Join us and instantly unlock extensive past papers & exclusive solutions to get a head start on your studies!