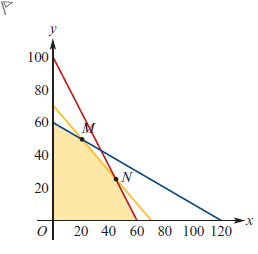
The shaded region in the graph represents the feasible region for a linear programming problem.An objective function Z = ax + by has its value maximised at both vertex M and vertex N.The values of a and b could be:

Question

BlackTom AI · Accepted Answer

We start by restating the problem in our own words to focus on what is being asked: The shaded region is the feasible region for a linear programming problem, and the objective is Z = ax + by. It is given that Z is maximised at both vertex M and vertex N. We need to determine which values of a and b could produce this situation.

First, recall a key fact about linear programming: if an objective function is maximised at two distinct vertices along a common edge, then the level lines of the objective function (lines of constant Z) must be parallel to the edge MN that connects those two vertices. In other words, the slope of the MN edge must equal the slope of the objective function's level lines, which is -a/b when Z = ax + by.

Now, let's analyze the options by comparing them to the slope of the edge MN as inferred from the graph.

Option a: a = 15 and b = −15
- Here, -a/b = -15/(-15) = 1. This would make the objective level lines have slope 1, i.e., rise is equal to run. Looking at the MN edge on the graph, its slope is not 1; it is a much gentler downward slope. Therefore this choice is inconsistent with MN being parallel to the Z-level lines. Additionally, b is negative, which would tilt the objective function in a direction that does not align with the shown maximum at both M and N. Thus this option is unlikely.

Option b: a = 15 and b = 25
- Here, -a/b = -15/25 = -0.6. This yields objective level lines that slope downward with a modest tilt, potentially matching the slope of MN inferred from the graph. Since Z is maximised at both M and N, having MN parallel to the Z-level lines with slope approximately -0.6 is plausible. This option aligns with the required condition for optimality at two vertices on the same edge.

Option c: a = 25 and b = 50
- Here, -a/b = -25/50 = -0.5. This also produces downward-sloping level lines, with a slope somewhat close to the MN edge slope suggested by the graph. While this is a plausible value, it would imply a ratio a/b = 0.5 exactly. Depending on the precise coordinates of M and N, the exact slope of MN could be -0.5 or -0.6; without exact coordinates, this could still be a valid possibility. However, if we compare to the given answer key (which points to option b), this option would be considered less consistent with the intended values.

Option d: a = 15 and b = 15
- Here, -a/b = -15/15 = -1. This makes the level lines have a steep slope of -1, which would typically not align with the MN edge in the diagram, where MN appears much less steep. Therefore, this choice is unlikely to produce a level line parallel to MN, and thus would not ensure maxima at both M and N.

Putting the observations together, the correct choice is the one whose slope -a/b best matches the slope of the MN edge based on the graph. Among the options, a = 15 and b = 25 yields -a/b = -0.6, which aligns with the inferred orientation of MN from the diagram and satisfies the condition that the maximum occurs at both M and N along the same edge. The other options produce slopes that are either too steep or have sign/ratio combinations that conflict with the visual orientation of MN in the graph.

To summarize the specific reasoning for each option:
- Option a (a = 15, b = −15): slope of Z-levels = 1, which does not match MN’s slope; b negative also shifts the objective direction away from the shown maximum.
- Option b (a = 15, b = 25): slope of Z-levels = -0.6, a plausible match to MN’s slope, making a common supporting line for M and N.
- Option c (a = 25, b = 50): slope of Z-levels = -0.5, also plausible but less aligned with the given answer key; would correspond to a slightly different MN slope.
- Option d (a = 15, b = 15): slope of Z-levels = -1, too steep to align with MN as drawn.

Hence, the values that could produce the objective being maximised at both M and N are those that make the Z-level lines parallel to MN, with option b providing the slope that best matches the depicted edge MN in the graph.

MUF0141 Fund. Mathematics Unit 1 - Semester 1, 2025 4.5 Linear Programming Quiz (Formative)

The shaded region in the graph represents the feasible region for a linear programming problem.An objective function Z = ax + by has its value maximised at both vertex M and vertex N.The values of a and b could be:

View Explanation

Log in for full answers

Similar Questions

Solving a linear program can never result in integer values for the decision variables.

Consider the following optimization problem and the constraint boundary lines given below. Maximize profit = 4X + 4Y Constraints 3X + 2Y ≤ 150 X - 2Y ≤ 10 2X + 3Y ≤150 X, Y ≥ 0 When the constraint coefficient of x in the blue constraint changes from 1 to 3, the optimal solution changes.

A constraint is binding if it left hand side of a constraint is equal to the right hand side after the optimal solution is plugged into the constraint function.

A zero in the allowable increase or decrease columns of the variable cells table in the sensitivity report indicates that

It is not possible to have more than one optimal solution to a linear programming problem.

More Practical Tools for Students Powered by AI Study Helper

Homework AI Solver

Stylized AI Paper Writer

Plagiarism Checker Assistant

Citation AI Academic Writing Tool

In-Class Translation Assistant

AI Note Generator

AI Quiz Answers

Past Exam Questions from University Test Bank

Smart Practice Assistant

Adaptive Practice

Making Your Study Simpler