Questions
Questions

业务建模与优化 - DAT-3659 - BMBAN2 A3. 1 课堂测验 01 - 业务建模和优化测验 1（远程监考）

Single choice

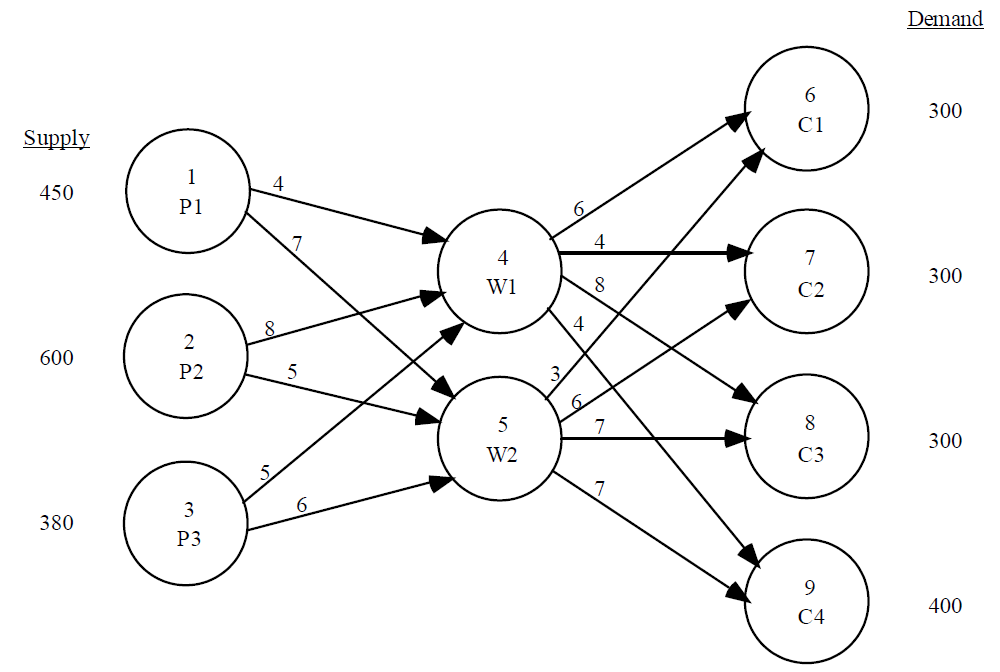
下图中，关于线性规划问题，下列哪项说法是错误的？标有 Z* 的点是最佳解决方案。

Question Image
View Explanation

View Explanation

Verified Answer
Please login to view
Step-by-Step Analysis
题干内容用中文给出：在下图所示的线性规划问题中，关于“标有 Z* 的点是最佳解决方案”的描述，下面哪一项是错误的？选项只有一个： - 约束 B 具有约束力。 对每个选项进行分析如下： 选项：约束 B 具有约束力。 - 这个陈述在图中并未明确标出“约束 B”的具体边界、哪一个供......Login to view full explanation

Log in for full answers

We've collected over 50,000 authentic exam questions and detailed explanations from around the globe. Log in now and get instant access to the answers!

Similar Questions

Solving a linear program can never result in integer values for the decision variables. 

Consider the following optimization problem and the constraint boundary lines given below. Maximize profit = 4X + 4Y  Constraints 3X + 2Y ≤ 150 X - 2Y ≤ 10 2X + 3Y ≤150 X, Y ≥ 0 If we increase the objective function coefficient of x by 2, i.e., 4 becomes 6, the new optimal solution includes point C.

Consider the following optimization problem and the constraint boundary lines given below. Maximize profit = 4X + 4Y  Constraints 3X + 2Y ≤ 150 X - 2Y ≤ 10 2X + 3Y ≤150 X, Y ≥ 0 When the constraint coefficient of x in the blue constraint changes from 1 to 3, the optimal solution changes. 

Consider the following Excel sensitivity report and it's accompanying problem:   Minimize cost = X + 2Y    subject to  X + 3Y ≥ 90   8X + 2Y ≥ 160    3X + 2Y ≥120    Y ≤ 70    X, Y≥ 0   Variable Cells                     Final Reduced Objective Allowable Allowable   Cell Name Value Cost Coefficient Increase Decrease   $B$3 X 25.71 0 1 2 0.333333333   $C$3 Y 21.43 0 2 1 1.333333333                 Constraints                     Final Shadow Constraint Allowable Allowable   Cell Name Value Price R.H. Side Increase Decrease   $J$6           LHS 90 0.57 90 62 50   $J$7           LHS 248.57 0 160 88.57142857 1E+30   $J$8           LHS 120 0.14 120 150 28.18181818   $J$9           LHS 21.43 0 70 1E+30 48.57142857   Suppose we add another variable, x3, with an objective function coefficient of 9, and constraint coefficients of 8, 3, and 5 for the first three constraints, respectively. What is the marginal impact of this new variable on the objective function? (In your calculations round all the numbers to 2 decimals.)       

More Practical Tools for Students Powered by AI Study Helper

Join us and instantly unlock extensive past papers & exclusive solutions to get a head start on your studies!