Still overwhelmed by exam stress? You've come to the right place!
We know exam season has you totally swamped. To support your studies, access Gold Membership for FREE until December 31, 2025! Normally £29.99/month. Just Log In to activate – no strings attached.
Let us help you ace your exams efficiently!
Questions
BU.520.601.T2.FA25 Final Exam
True/False
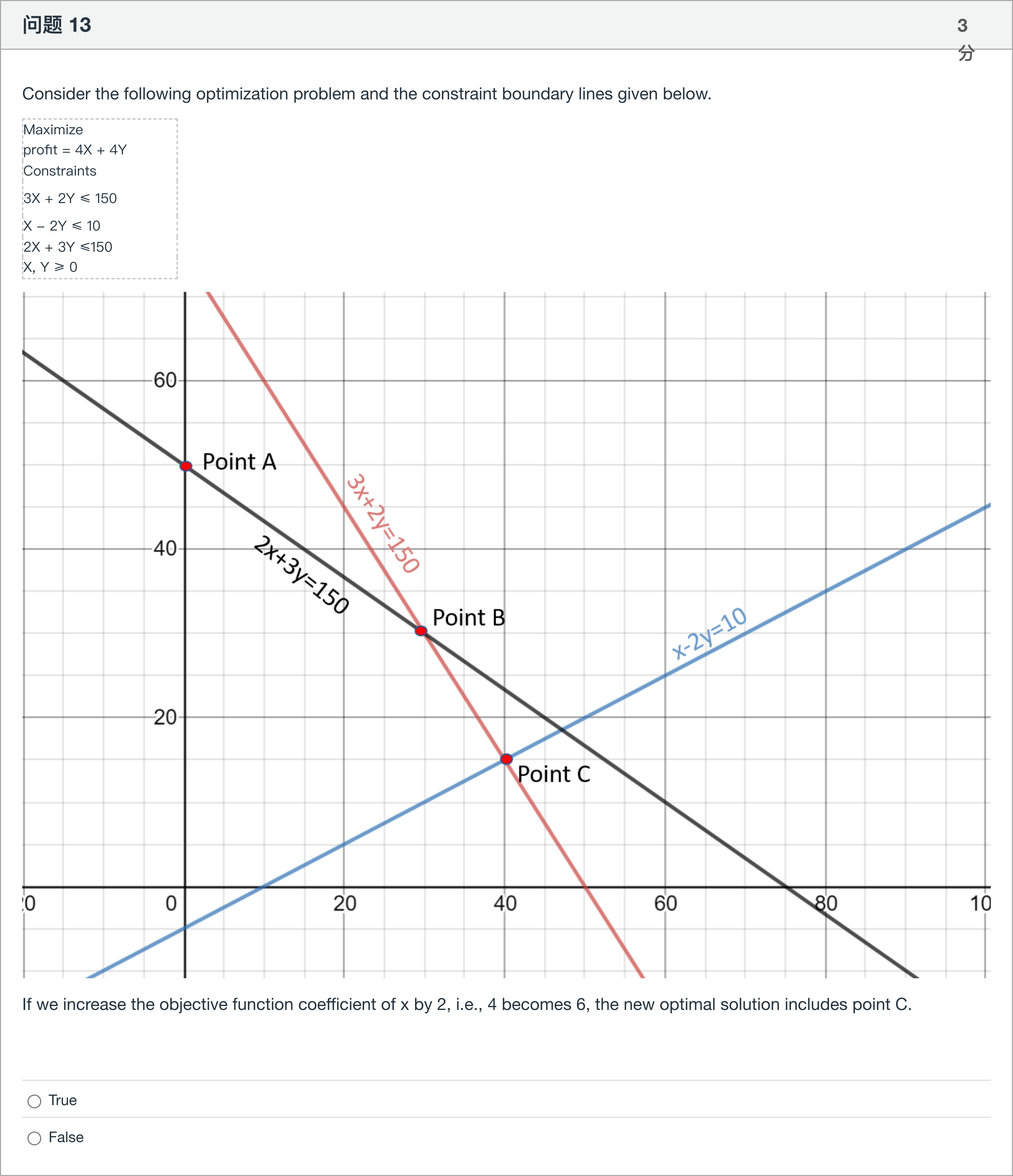
Consider the following optimization problem and the constraint boundary lines given below. Maximize profit = 4X + 4Y Constraints 3X + 2Y ≤ 150 X - 2Y ≤ 10 2X + 3Y ≤150 X, Y ≥ 0 If we increase the objective function coefficient of x by 2, i.e., 4 becomes 6, the new optimal solution includes point C.
Options
A.True
B.False
View Explanation
Standard Answer
Please login to view
Approach Analysis
Here is the problem restated: We have an optimization problem with Maximize profit = 4X + 4Y subject to the constraints 3X + 2Y ≤ 150, X − 2Y ≤ 10, 2X + 3Y ≤ 150, and X, Y ≥ 0. The statement claims that if we increase the objective function coefficient of x by 2 (from 4 to 6), the new optimal solution includes point C. The answer options are: True or False.
Option 1: True. This option asserts that increasing the coefficient of X in the objective function changes the optimal solution to include the point labeled C on the graph. To evaluate this, we consider how changing the objective coefficients affects the optimal vertex of the feasible region. When the profit coefficients change, the set of supporting hyperplanes (or iso-profit lines) rota......Login to view full explanationLog in for full answers
We've collected over 50,000 authentic exam questions and detailed explanations from around the globe. Log in now and get instant access to the answers!
Similar Questions
Solving a linear program can never result in integer values for the decision variables.
Consider the following optimization problem and the constraint boundary lines given below. Maximize profit = 4X + 4Y Constraints 3X + 2Y ≤ 150 X - 2Y ≤ 10 2X + 3Y ≤150 X, Y ≥ 0 When the constraint coefficient of x in the blue constraint changes from 1 to 3, the optimal solution changes.
Consider the following Excel sensitivity report and it's accompanying problem: Minimize cost = X + 2Y subject to X + 3Y ≥ 90 8X + 2Y ≥ 160 3X + 2Y ≥120 Y ≤ 70 X, Y≥ 0 Variable Cells Final Reduced Objective Allowable Allowable Cell Name Value Cost Coefficient Increase Decrease $B$3 X 25.71 0 1 2 0.333333333 $C$3 Y 21.43 0 2 1 1.333333333 Constraints Final Shadow Constraint Allowable Allowable Cell Name Value Price R.H. Side Increase Decrease $J$6 LHS 90 0.57 90 62 50 $J$7 LHS 248.57 0 160 88.57142857 1E+30 $J$8 LHS 120 0.14 120 150 28.18181818 $J$9 LHS 21.43 0 70 1E+30 48.57142857 Suppose we add another variable, x3, with an objective function coefficient of 9, and constraint coefficients of 8, 3, and 5 for the first three constraints, respectively. What is the marginal impact of this new variable on the objective function? (In your calculations round all the numbers to 2 decimals.)
A constraint is binding if it left hand side of a constraint is equal to the right hand side after the optimal solution is plugged into the constraint function.
More Practical Tools for International Students
Making Your Study Simpler
To make preparation and study season easier for more international students, we've decided to open up Gold Membership for a limited-time free trial until December 31, 2025!