Questions
Numerical
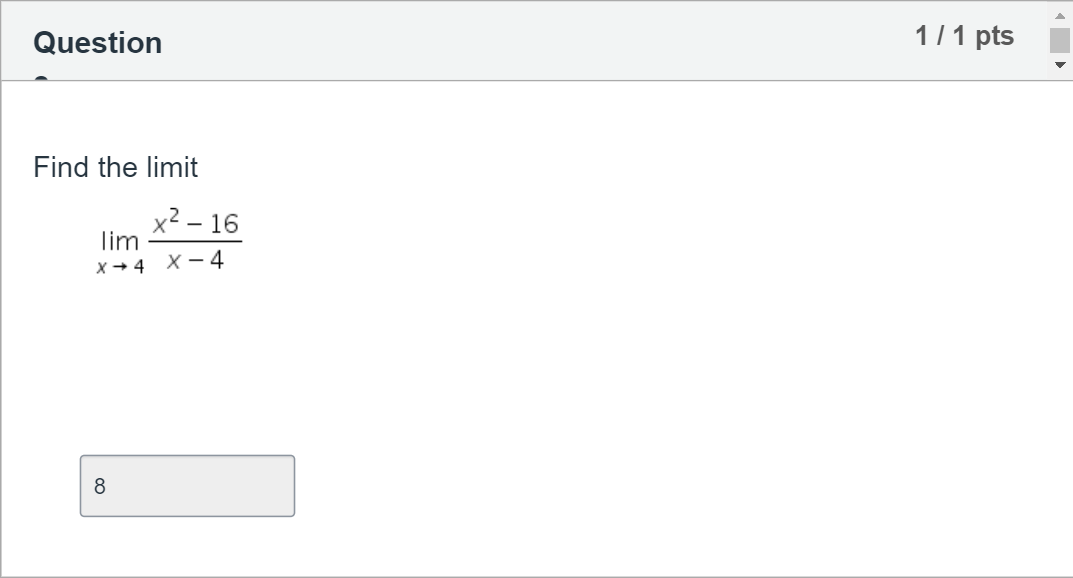
Find the limit
View Explanation
Verified Answer
Please login to view
Step-by-Step Analysis
To begin, observe the expression inside the limit: (x^2 - 16) / (x - 4).
Next, factor the numerator as a difference of squares: x^2 - 1......Login to view full explanationLog in for full answers
We've collected over 50,000 authentic exam questions and detailed explanations from around the globe. Log in now and get instant access to the answers!
Similar Questions
NOTE: Due to formatting constraints, limits are shown with a horizontal bar in these quiz questions.For example: will be written as: \( \frac{lim}{x \rightarrow a }f(x) \)Solve the following limit and write your answer to three decimal places.\( \frac{lim}{x \rightarrow 2 } (\frac{x^3+7x^2-18x}{x^2-4}) \)
NOTE: Due to formatting constraints, limits are shown with a horizontal bar in these quiz questions.For example: will be written as: \( \frac{lim}{x \rightarrow a }f(x) \)Solve the following limit and write your answer to three decimal places.\( \frac{lim}{x \rightarrow \infty } (\frac{2x^2+4x+-6}{-2x^2+-7x+10}) \)
NOTE: Due to formatting constraints, limits are shown with a horizontal bar in these quiz questions.For example: will be written as: [math: limx→af(x)] \frac{lim}{x \rightarrow a }f(x) Solve the following limit and write your answer to three decimal places.[math: limx→2(x3+7x2−18xx2−4)] \frac{lim}{x \rightarrow 2 } (\frac{x^3+7x^2-18x}{x^2-4})
NOTE: Due to formatting constraints, limits are shown with a horizontal bar in these quiz questions.For example: will be written as: [math: limx→af(x)] \frac{lim}{x \rightarrow a }f(x) Solve the following limit and write your answer to three decimal places.[math: limx→9(x+7x+9)] \frac{lim}{x \rightarrow 9 } (\frac{x+7}{x+9})
More Practical Tools for International Students
Making Your Study Simpler
Join us and instantly unlock extensive past papers & exclusive solutions to get a head start on your studies!