Questions
MCD2130 - T2 - 2025 Lecture Task Week 5
Single choice
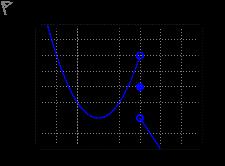
Question text Consider the graph of [math: f(x)] shown below: a) [math: limx→2−f(x)=]\displaystyle \lim_{{x \to {2}^-}} f(x) =[input] b) [math: limx→2+f(x)=]\displaystyle\lim_{{x \to {2}^+}} f(x) =[input] c) [math: limx→2f(x)=]\displaystyle\lim_{{x \to {2}}} f(x) =[select: (Clear my choice), does not exist., exists and equals 1] Check Question 1
View Explanation
Verified Answer
Please login to view
Step-by-Step Analysis
First, restate the problem as given: we are asked to evaluate three one-sided and two-sided limits at x = 2 from the graph provided. The options shown are: a) lim_{x→2−} f(x) = [input], b) lim_{x→2+} f(x) = [input], c) lim_{x→2} f(x) = [select: Clear my choice, does not exist., exists and equals 1]. Now we analyze each piece.
Option a) lim_{x→2−} f(x) = 1. To assess the left-hand limit, observe the graph as x approaches 2 from values less than 2. If the y-value the graph approaches from the left-hand side is 1, this option would be correct. We need to check whether the left branch of the graph indeed approaches the height y ......Login to view full explanationLog in for full answers
We've collected over 50,000 authentic exam questions and detailed explanations from around the globe. Log in now and get instant access to the answers!
Similar Questions
Which of the following statements must be true, and which are false? Note: each part is independent from the others. a) If 𝑓 ( 𝑥 ) is a polynomial, then lim 𝑥 → 5 𝑓 ( 𝑥 ) can be evaluated by computing 𝑓 ( 5 ) . [ Select ] False True b) If 𝑅 ( 𝑥 ) is a rational function, then lim 𝑥 → 7 𝑅 ( 𝑥 ) can be evaluated by computing 𝑅 ( 7 ) . [ Select ] False True c) If 𝑝 ( 𝑥 ) is a polynomial, then lim 𝑥 → 5 + 𝑝 ( 𝑥 ) can be evaluated by computing 𝑝 ( 5 ) . [ Select ] True False d) If 𝑓 ( 2 ) = 4 then lim 𝑥 → 2 [ 𝑓 ( 𝑥 ) ] 2 = 16 [ Select ] False True e) If lim 𝑥 → 4 ( 5 𝑓 ( 𝑥 ) ) = 15 , then lim 𝑥 → 4 𝑓 ( 𝑥 ) = 3 . [ Select ] True False f) If lim 𝑥 → 4 ( 𝑥 𝑓 ( 𝑥 ) ) = 8 , then lim 𝑥 → 4 𝑓 ( 𝑥 ) = 2 . [ Select ] False True
the graph of f(x)f\left(x\right) given above. Use it to find the following one-sided and two-sided limits. (If a limit does not exist, write DNE.) limx→1−f(x)=\lim\limits_{x\:\rightarrow1^-}\:f\left(x\right)= [Fill in the blank], limx→1+f(x)=\lim\limits_{x\rightarrow1^+}f\left(x\right)= [Fill in the blank], limx→1f(x)=\lim\limits_{x\rightarrow1}f\left(x\right)\:= [Fill in the blank], limx→2f(x)=\lim\limits_{x\rightarrow2}f\left(x\right)= [Fill in the blank], limx→3−f(x)=\lim\limits_{x\rightarrow3^-}f\left(x\right)= [Fill in the blank], limx→3f(x)=\lim\limits_{x\rightarrow3}f\left(x\right)=[Fill in the blank], limx→4f(x)=\lim\limits_{x\rightarrow4}f\left(x\right)=[Fill in the blank],
Consider the two graphs above. What are the following limits? (If a limit does not exist, write DNE.) limx→1f(x)=\lim\limits_{x\rightarrow1}f\left(x\right)= [Fill in the blank], limx→1g(x)=\lim\limits_{x\rightarrow1}g\left(x\right)= [Fill in the blank], Note that the two functions f(x)f\left(x\right) and g(x)g\left(x\right) are identical except for at x=1x=1 . Is the following statement TRUE or FALSE? For any function h(x)h\left(x\right) , the limit limx→ah(x)\lim\limits_{x\rightarrow a}h\left(x\right) does not depend on the value of h(x)h\left(x\right) at x=ax=a , or even whether h(a)h\left(a\right) is defined or not. [Fill in the blank], (Write "TRUE" or "FALSE".)
Question text Consider the function [math: f(x)={3x+5,x<33x2+4x−2,x≥3] f(x)= \begin{cases} \displaystyle & {3\,x+5}, & x < {3} \\ & {3\,x^2+4\,x-2}, & x \geq {3}\end{cases} . a) [math: limx→3−f(x)=]\displaystyle \lim_{{x \to {3}^-}} f(x) = [input] b) [math: limx→3+f(x)=]\displaystyle\lim_{{x \to {3}^+}} f(x) = [input] c) [math: limx→3f(x)=]\displaystyle\lim_{{x \to {3}}} f(x) = [select: (Clear my choice), does not exist since left limit is not equal to right limit., exists and equals 37] Check Question 3
More Practical Tools for Students Powered by AI Study Helper
Making Your Study Simpler
Join us and instantly unlock extensive past papers & exclusive solutions to get a head start on your studies!