Questions
Single choice
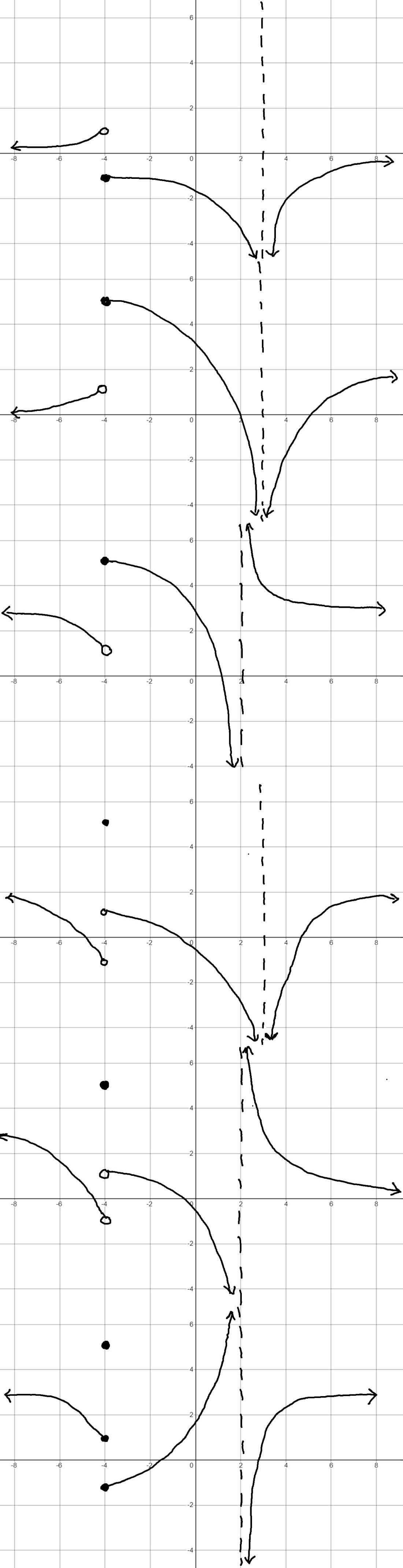
Determine which graph satisfies all of the following conditions: lim 𝑥 ⟶ − 4 − 𝑓 ( 𝑥 ) = − 1 lim 𝑥 ⟶ − 4 + 𝑓 ( 𝑥 ) = 1 lim 𝑥 ⟶ 3 𝑓 ( 𝑥 ) = − ∞ lim 𝑥 ⟶ − ∞ 𝑓 ( 𝑥 ) = 2 lim 𝑥 ⟶ + ∞ 𝑓 ( 𝑥 ) = 2 𝑓 ( − 4 ) = 5
Options
A.
B.
C.
D.
E.
F.
View Explanation
Verified Answer
Please login to view
Step-by-Step Analysis
To determine which graph satisfies all given conditions, let's parse each condition and compare it to the features a graph would need to display.
- Condition: lim_{x -> -4^-} f(x) = -1 and lim_{x -> -4^+} f(x) = 1, with f(-4) = 5.
This implies a jump discontinuity at x = -4: the left-hand limit should approach -1, the right-hand limit should approach 1, and there should be a solid point at x = -4 with y = 5 indicating the function value there.
A correct graph must show a vertical gap or jump as x passes -4, with the two one-sided limits approaching the specified values, and ......Login to view full explanationLog in for full answers
We've collected over 50,000 authentic exam questions and detailed explanations from around the globe. Log in now and get instant access to the answers!
Similar Questions
Suppose that with a certain phone company, an international long distance phone call from Canada to Brazil costs $0.90 for the first minute (up to and including 60 seconds), plus $0.50 for each additional minute or part of a minute. Note: "Part of a minute" means that if a new minute is started even just by one second, a full minute is charged. For example, a 5 min 1 sec phone call costs the same as a 5 min 50 sec phone call and the same as a 6 min 0 sec phone call. Suppose 𝐶 ( 𝑡 ) is the function that gives the cost of making a 𝑡 minute long phone call. On a piece of paper, sketch a graph showing 𝐶 ( 𝑡 ) (with 𝐶 on the 𝑦 -axis and 𝑡 on the 𝑥 -axis). Then use your graph to evaluate each of the following: (Write DNE for undefined.) 𝐶 ( 2.5 ) = [ Select ] DNE 1.9 1.4 2.4 2.9 𝐶 ( 4 ) = [ Select ] 3.4 1.9 2.9 2.4 DNE lim 𝑥 → 3.1 𝐶 ( 𝑡 ) = [ Select ] 1.9 1.4 2.9 2.4 DNE lim 𝑥 → 4 − 𝐶 ( 𝑡 ) = [ Select ] 2.4 1.4 2.9 1.9 DNE lim 𝑥 → 4 + 𝐶 ( 𝑡 ) = [ Select ] DNE 2.9 2.4 3.4 1.9 lim 𝑥 → 4 𝐶 ( 𝑡 ) = [ Select ] 1.9 2.9 DNE 3.4 2.4
Consider this graph of the function 𝑓 ( 𝑥 ) . Which of the following statements are true and which are false? lim 𝑥 → 3 − 𝑓 ( 𝑥 ) = lim 𝑥 → 3 + 𝑓 ( 𝑥 ) [ Select ] False True lim 𝑥 → 1 𝑓 ( 𝑥 ) = 𝑓 ( 1 ) [ Select ] True False 𝑓 ( 𝑥 ) has a vertical asymptote at 𝑥 = 4 . [ Select ] False True 𝑓 ( 𝑥 ) has a vertical asymptote at 𝑥 = 6 . [ Select ] False True lim 𝑥 → 4 − 𝑓 ( 𝑥 ) = lim 𝑥 → 4 + 𝑓 ( 𝑥 ) [ Select ] False True lim 𝑥 → 4 𝑓 ( 𝑥 ) = ∞ [ Select ] True False lim 𝑥 → 6 𝑓 ( 𝑥 ) = ∞ [ Select ] False True The limit lim 𝑥 → 4 𝑓 ( 𝑥 ) exists, but lim 𝑥 → 6 𝑓 ( 𝑥 ) does not exist. [ Select ] False True
Consider the function 𝑓 ( 𝑥 ) = { 𝑥 2 + 1 𝑖 𝑓 𝑥 < 2 3 𝑖 𝑓 𝑥 = 2 7 − 𝑥 𝑖 𝑓 𝑥 > 2 . We aim to find out if 𝑓 ( 𝑥 ) has a discontinuity at 𝑥 = 2 , and if so, of what type. In order to do that, first find the following information: 𝑓 ( 2 ) = [ Select ] 5 3 2 7 lim 𝑥 ⟶ 2 − 𝑓 ( 𝑥 ) = [ Select ] 7 3 2 5 lim 𝑥 ⟶ 2 + 𝑓 ( 𝑥 ) = [ Select ] 5 7 2 3 Is 𝑓 ( 𝑥 ) continuous or discontinuous at 𝑥 = 2 ? [ Select ] discontinuous continuous If 𝑓 ( 𝑥 ) is discontinuous at 𝑥 = 2 , what type of discontinuity is it? [ Select ] f is continuous An infinite discontinuity A removable discontinuity A jump discontinuity
Consider this graph of the function 𝑓 ( 𝑥 ) . Which of the following statements are true and which are false? lim 𝑥 → 3 − 𝑓 ( 𝑥 ) = lim 𝑥 → 3 + 𝑓 ( 𝑥 ) [ Select ] False True lim 𝑥 → 1 𝑓 ( 𝑥 ) = 𝑓 ( 1 ) [ Select ] False True 𝑓 ( 𝑥 ) has a vertical asymptote at 𝑥 = 4 . [ Select ] True False 𝑓 ( 𝑥 ) has a vertical asymptote at 𝑥 = 6 . [ Select ] False True lim 𝑥 → 4 − 𝑓 ( 𝑥 ) = lim 𝑥 → 4 + 𝑓 ( 𝑥 ) [ Select ] True False lim 𝑥 → 4 𝑓 ( 𝑥 ) = ∞ [ Select ] False True lim 𝑥 → 6 𝑓 ( 𝑥 ) = ∞ False The limit lim 𝑥 → 4 𝑓 ( 𝑥 ) exists, but lim 𝑥 → 6 𝑓 ( 𝑥 ) does not exist. [ Select ] True False
More Practical Tools for Students Powered by AI Study Helper
Making Your Study Simpler
Join us and instantly unlock extensive past papers & exclusive solutions to get a head start on your studies!