Still overwhelmed by exam stress? You've come to the right place!
We know exam season has you totally swamped. To support your studies, access Gold Membership for FREE until December 31, 2025! Normally £29.99/month. Just Log In to activate – no strings attached.
Let us help you ace your exams efficiently!
Questions
COMP4328 COMP5328 COMP8328 (NE) Week 4 quiz
Single choice
The law of large numbers describes the result of performing the same experiment a large number of times. Let be examples i.i.d. drawn from a distribution . Let be a function. Then which equation reflects the law of large numbers. A. lim 𝑛 → ∞ ∑ 𝑖 = 1 𝑛 𝑓 ( 𝑥 𝑖 ) = 𝐸 𝑋 ∼ 𝐷 [ 𝑓 ( 𝑋 ) ] . B. lim 𝑛 → ∞ 1 𝑛 ∑ 𝑖 = 1 𝑛 𝑓 ( 𝑥 𝑖 ) = 𝐸 𝑋 ∼ 𝐷 [ 𝑓 ( 𝑋 ) ] . C. lim 𝑛 → ∞ ∑ 𝑖 = 1 𝑛 𝑓 ( 𝑥 𝑖 ) = 𝑓 ( 𝐸 𝑋 ∼ 𝐷 [ 𝑋 ] ) . D. lim 𝑛 → ∞ 1 𝑛 ∑ 𝑖 = 1 𝑛 𝑓 ( 𝑥 𝑖 ) = 𝑓 ( 𝐸 𝑋 ∼ 𝐷 [ 𝑋 ] ) . E. None of the above equations is true.
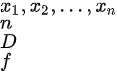
View Explanation
Standard Answer
Please login to view
Approach Analysis
The task presents a question about the law of large numbers (LLN) and provides a set of answer choices A–E, but the answer_options field is empty, so we don’t have the explicit text of each option to analyze individually. Nevertheless, we can reason about the LLN in general and evaluate the likely structure of the statements.
First, recall the standard statement of the law of large numbers in this context: if X1, X2, ..., Xn are i.i.d. samples from a distribution D, and f is a function with a finite expectation E[f(X)], then the sample average converges to the expected val......Login to view full explanationLog in for full answers
We've collected over 50,000 authentic exam questions and detailed explanations from around the globe. Log in now and get instant access to the answers!
Similar Questions
Select all statements that are correct. The law of large numbers and central limit theorem (taken together) imply that:
As the sample size increases, the expected value of noise Stays the Same
Which of the following statements is true about the Law of Large Numbers?
Consider two pairs of grandparents. The first pair has 4 grandchildren and the second pair has 31 grandchildren. Which of the two pairs is more likely to have between 40% and 60% boys as grandchildren, assuming that boys and girls are equally likely as children? Why?
More Practical Tools for International Students
Making Your Study Simpler
To make preparation and study season easier for more international students, we've decided to open up Gold Membership for a limited-time free trial until December 31, 2025!