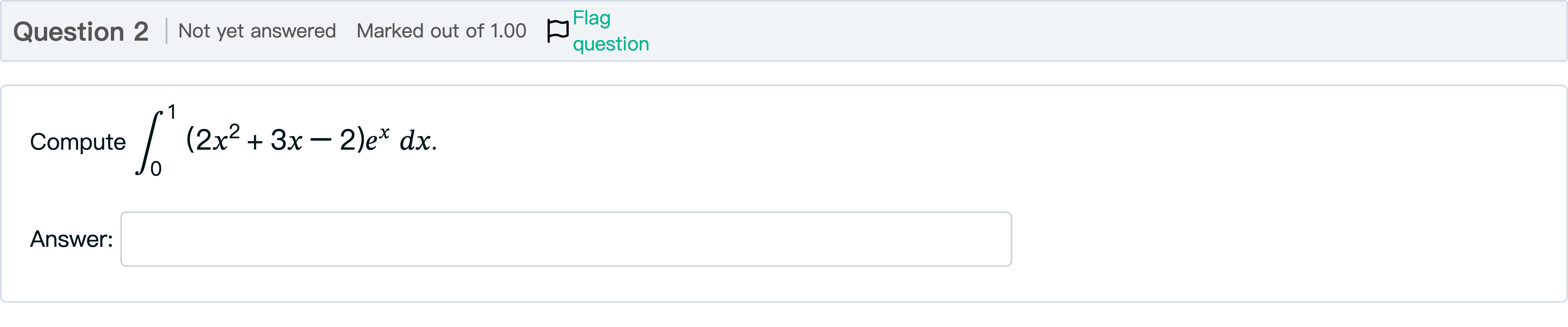
Compute [math: ∫01(2x2+3x−2)ex dx]\displaystyle \int _0^1{(2x^2+3x-2)e^x dx}.

Question

BlackTom AI · Accepted Answer

We start by considering the definite integral: ∫ from 0 to 1 of (2x^2 + 3x − 2) e^x dx.

Step 1: Apply integration by parts to separate the polynomial from e^x. Let u = 2x^2 + 3x − 2 and dv = e^x dx. Then du = (4x + 3) dx and v = e^x.

Thus ∫_0^1 (2x^2 + 3x − 2) e^x dx = [ (2x^2 + 3x − 2) e^x ]_0^1 − ∫_0^1 (4x + 3) e^x dx.

Step 2: Evaluate the boundary term: (2x^2 + 3x − 2) e^x at x = 1 and x = 0.
- At x = 1: (2(1)^2 + 3(1) − 2) e^1 = (2 + 3 − 2) e = 3e.
- At x = 0: (2(0)^2 + 3(0) − 2) e^0 = (−2) · 1 = −2.
So the boundary term is 3e − (−2) = 3e + 2.

Step 3: Compute the remaining integral ∫_0^1 (4x + 3) e^x dx using integration by parts again. Let u = 4x + 3 and dv = e^x dx, so du = 4 dx and v = e^x.
Then ∫ (4x + 3) e^x dx = (4x + 3) e^x − ∫ 4 e^x dx = (4x + 3) e^x − 4 e^x = (4x − 1) e^x.
Evaluate from 0 to 1: [(4x − 1) e^x]_0^1 = (4·1 − 1) e^1 − (4·0 − 1) e^0 = 3e − (−1) = 3e + 1.

Step 4: Put everything together.
∫_0^1 (2x^2 + 3x − 2) e^x dx = (boundary term) − (second integral) = (3e + 2) − (3e + 1) = 1.

Thus the computed value of the integral is 1.

_MATH1013_1ABCD_2025 Subsection 5.2 (closed on 15 Nov)

Compute [math: ∫01(2x2+3x−2)ex dx]\displaystyle \int _0^1{(2x^2+3x-2)e^x dx}.

View Explanation

Log in for full answers

Similar Questions

(a) Integrate the following (i) (Hint: You may substitute , and adopt integration by parts) [2 marks](ii) (Hint: You may let , , use and adopt integration by parts)[2 marks] (b) Differentiate [3 marks][Fill in the blank]

Question at position 9 ∫033xex3dx=\int_0^33xe^{\frac{x}{3}}dx=903276

Use of integration by parts \displaystyle\int f(x)\,g'(x)\,dx=f(x)\,g(x) - \displaystyle \int f'(x)\,g(x)\,dxrequires a suitable choice for f(x) and g'(x).Choose from the options below, the choice of f(x) and g'(x) that will NOT help find the corresponding indefinite integral.

Integration by parts [math: ∫f′(x)g(x)dx=f(x)g(x)−∫f(x)g′(x)dx]\int f'(x) g(x) \, dx = f(x) g(x) - \int f(x) g'(x) \, dx is the partial integral counterpart to which of the following rules?

Integration by parts \[\int f'(x) g(x) \, dx = f(x) g(x) - \int f(x) g'(x) \, dx \] is the partial integral counterpart to which of the following rules?

More Practical Tools for Students Powered by AI Study Helper

Homework AI Solver

Stylized AI Paper Writer

Plagiarism Checker Assistant

Citation AI Academic Writing Tool

In-Class Translation Assistant

AI Note Generator

AI Quiz Answers

Past Exam Questions from University Test Bank

Smart Practice Assistant

Adaptive Practice

Making Your Study Simpler