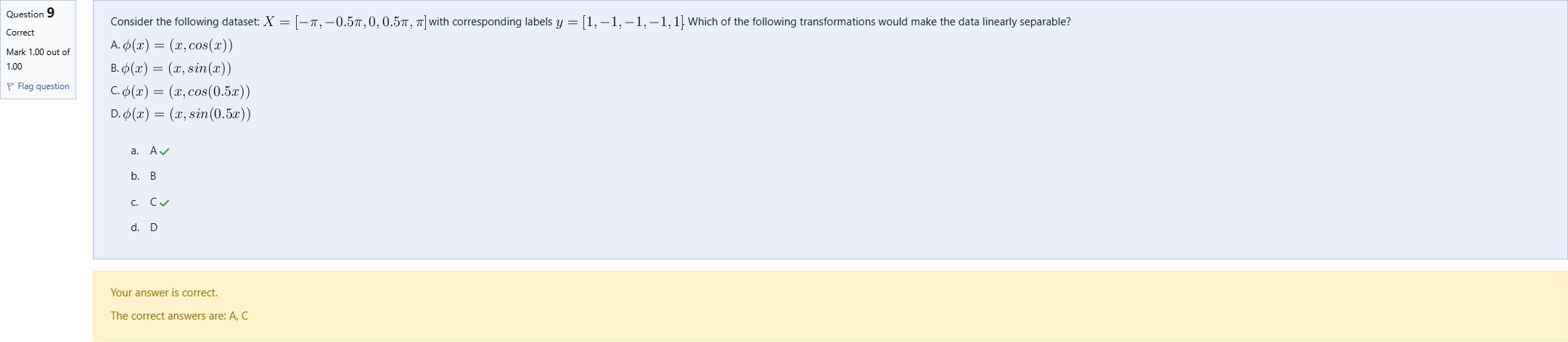
Consider the following dataset: X=[-\pi,-0.5\pi,0,0.5\pi,\pi] with corresponding labels y=[1,-1,-1,-1,1]. Which of the following transformations would make the data linearly separable? A. \phi(x)=(x,cos( x)) B. \phi(x)=(x,sin(x)) C. \phi(x)=(x,cos(0.5 x)) D. \phi(x)=(x,sin(0.5 x))

Question

BlackTom AI · Accepted Answer

Question restatement: Given X = [-π, -0.5π, 0, 0.5π, π] with labels y = [1, -1, -1, -1, 1], which of the following feature mappings φ(x) would make the data linearly separable?
Options:
A. φ(x) = (x, cos(x))
B. φ(x) = (x, sin(x))
C. φ(x) = (x, cos(0.5x))
D. φ(x) = (x, sin(0.5x))

Option-by-option analysis:
A) φ(x) = (x, cos(x))
- Intuition: Adding a cosine term can introduce nonlinear curvature that might separate the symmetric labels at the chosen x values. The cos(x) component oscillates between -1 and 1 with the same period as x’s domain here, which can create a decision boundary in the (x, cos x) feature space that splits the two classes more easily than in the original x-space.
- Why this could work: The first coordinate x preserves the ordering and magnitude information, while cos(x) adds a nonlinear pairing that can tilt the decision boundary to place the positive labels at -π and π on one side and the -1 labels in between on the other side.
- Potential caveat: The separability depends on the exact learned hyperplane in the augmented space, but at these specific x values the added cos(x) feature can provide a separating arrangement.

B) φ(x) = (x, sin(x))
- Intuition: The sine term sin(x) is also a bounded nonlinear function, but its phase relative to the labels matters. For the given symmetric points, sin(x) yields zeros at x = 0 and ±π, with ±1 at ±π/2, which may not align to produce a clean linear separator with the x feature.
- Why this might fail: The combination (x, sin(x)) could still leave a margin where the two classes overlap in the (x, sin x) plane, making a single linear decision boundary insufficient to separate y = 1 at the endpoints from y = -1 in the interior.

C) φ(x) = (x, cos(0.5x))
- Intuition: Using cos(0.5x) changes the frequency of the nonlinear component compared to cos(x). This slower variation relative to x may create a distinctly curved boundary that more effectively separates the endpoints (x = ±π) from the interior points, due to phase and amplitude interactions with the linear x term.
- Why this could work: The cos(0.5x) term introduces a different nonlinear shape that can align with the target labels, especially since cos(0.5x) remains smooth and can create a separation in the augmented feature space by bending the decision boundary to place +1 at x = ±π while keeping -1 inside.

D) φ(x) = (x, sin(0.5x))
- Intuition: The sin(0.5x) term is a lower-frequency sine, introducing another smooth nonlinear component. However, for the specific data points, the sine term may not provide the necessary orientation or curvature to separate the endpoints from the interior reliably when paired with the linear x term.
- Why this might fail: The resulting decision boundary in (x, sin(0.5x)) space could still overlap the classes at some points or fail to flip the labeling order along the curve, leading to non-separability in the augmented space.

Summary of reasoning across options:
- The two mappings A and C incorporate nonlinear components that adjust the feature space in beneficial ways for linear separation given these particular x-values and labels. The cos(x) option (A) offers a direct nonlinear relationship that can help separate endpoints from interior points, while the cos(0.5x) option (C) provides a different nonlinear pattern via a lower-frequency cosine, which can also yield a linearly separable arrangement in the augmented space.
- The sine-based mappings (B and D) introduce nonlinearities as well, but their specific phase and symmetry with respect to the dataset do not guarantee a clear linear separator in the augmented space for these points, making them less reliable in this scenario.

Therefore, the potential linear separability is achieved by options A and C, given the described feature augmentations and the particular data configuration.

COMP9417-Machine Learning & Data Mining - T3 2025

Consider the following dataset: X=[-\pi,-0.5\pi,0,0.5\pi,\pi] with corresponding labels y=[1,-1,-1,-1,1]. Which of the following transformations would make the data linearly separable? A. \phi(x)=(x,cos( x)) B. \phi(x)=(x,sin(x)) C. \phi(x)=(x,cos(0.5 x)) D. \phi(x)=(x,sin(0.5 x))

View Explanation

Log in for full answers

Similar Questions

Let [math: x=(x1,x2)]x=(x_1,x_2) and [math: y=(y1,y2)]y=(y_1,y_2) and let kernel k be defined as follows: [math: k(x,y)=ex1x2+y1y2+2x1y1x2y2+0.25x13y13]k(x,y) = e^{x_1x_2+y_1y_2} +2 \frac{x_1 y_1}{x_2y_2} + 0.25 x_1^3 y_1^3 which transformation [math: ϕ]\phi does this kernel correspond to?

Let x=(x_1,x_2) and y=(y_1,y_2) and let kernel k be defined as follows: k(x,y) = e^{x_1x_2+y_1y_2} +2 \frac{x_1 y_1}{x_2y_2} + 0.25 x_1^3 y_1^3 which transformation \phi does this kernel correspond to?

Let [math: x=(x1,x2)]x=(x_1,x_2) and [math: y=(y1,y2)]y=(y_1,y_2) and let kernel k be defined as follows: [math: k(x,y)=ex1x2+y1y2+2x1y1x2y2+0.25x13y13]k(x,y) = e^{x_1x_2+y_1y_2} +2 \frac{x_1 y_1}{x_2y_2} + 0.25 x_1^3 y_1^3 which transformation [math: ϕ]\phi does this kernel correspond to?

Let [math: x=(x1,x2)]x=(x_1,x_2) and [math: y=(y1,y2)]y=(y_1,y_2) and let kernel k be defined as follows: [math: k(x,y)=ex1x2+y1y2+2x1y1x2y2+0.25x13y13]k(x,y) = e^{x_1x_2+y_1y_2} +2 \frac{x_1 y_1}{x_2y_2} + 0.25 x_1^3 y_1^3 which transformation [math: ϕ]\phi does this kernel correspond to?

More Practical Tools for Students Powered by AI Study Helper

Homework AI Solver

Stylized AI Paper Writer

Plagiarism Checker Assistant

Citation AI Academic Writing Tool

In-Class Translation Assistant

AI Note Generator

AI Quiz Answers

Past Exam Questions from University Test Bank

Smart Practice Assistant

Adaptive Practice

Making Your Study Simpler