Questions
COMP9417-Machine Learning & Data Mining - T3 2025
Multiple choice
Consider the following dataset: X=[−π,−0.5π,0,0.5π,π][math]X=[-\pi,-0.5\pi,0,0.5\pi,\pi] with corresponding labels y=[1,−1,−1,−1,1][math]y=[1,-1,-1,-1,1]. Which of the following transformations would make the data linearly separable? A. ϕ(x)=(x,cos(x))[math]\phi(x)=(x,cos( x)) B. ϕ(x)=(x,sin(x))[math]\phi(x)=(x,sin(x)) C. ϕ(x)=(x,cos(0.5x))[math]\phi(x)=(x,cos(0.5 x)) D. ϕ(x)=(x,sin(0.5x))[math]\phi(x)=(x,sin(0.5 x))
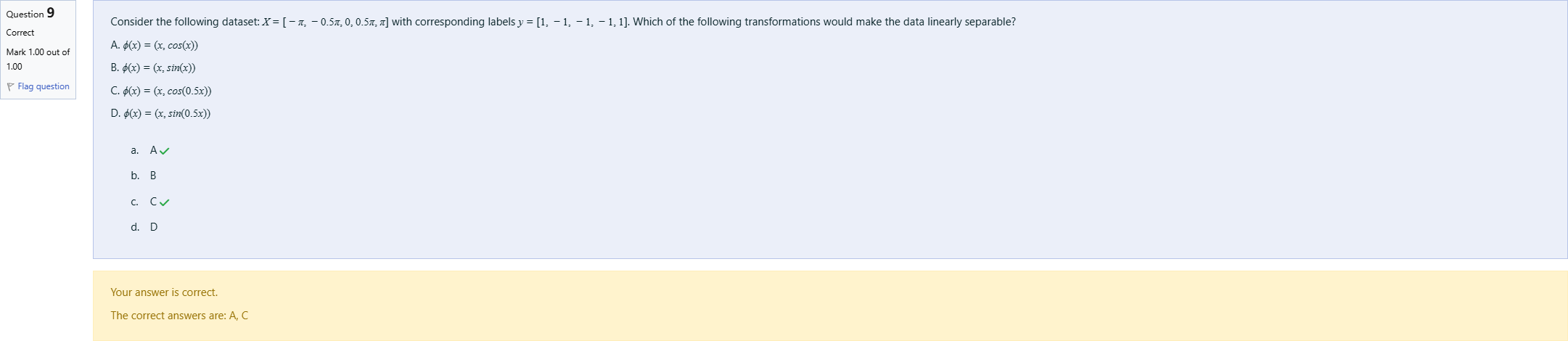
View Explanation
Verified Answer
Please login to view
Step-by-Step Analysis
We are given a dataset with X = [-π, -0.5π, 0, 0.5π, π] and labels y = [1, -1, -1, -1, 1]. We must evaluate which feature mappings φ(x) make the data linearly separable in the transformed feature space. Below, I analyze each option and explain why it would or would not yield linear separability.
Option A: φ(x) = (x, cos(x))
- Inspect the transformed points: the first coordinate is x, which takes values [-π, -0.5π, 0, 0.5π, π], and the second coordinate is cos(x), which yields [cos(-π)=-1, cos(-0.5π)=0, cos(0)=1, cos(0.5π)=0, cos(π)=-1]. So the transformed set is {(-π, -1), (-0.5π, 0), (0, 1), (0.5π, 0), (π, -1)} with labels {+1, -1, -1, -1, +1} respectively.
- A linear separator in 2D is a line ax + by + c = 0 that assigns +1 to some points and -1 to others. Visually, the two positive points lie at the far left and far right, both with second coordinates -1, while three negative points lie near the center with second......Login to view full explanationLog in for full answers
We've collected over 50,000 authentic exam questions and detailed explanations from around the globe. Log in now and get instant access to the answers!
Similar Questions
Let [math: x=(x1,x2)]x=(x_1,x_2) and [math: y=(y1,y2)]y=(y_1,y_2) and let kernel k be defined as follows: [math: k(x,y)=ex1x2+y1y2+2x1y1x2y2+0.25x13y13]k(x,y) = e^{x_1x_2+y_1y_2} +2 \frac{x_1 y_1}{x_2y_2} + 0.25 x_1^3 y_1^3 which transformation [math: ϕ]\phi does this kernel correspond to?
Let x=(x_1,x_2) and y=(y_1,y_2) and let kernel k be defined as follows: k(x,y) = e^{x_1x_2+y_1y_2} +2 \frac{x_1 y_1}{x_2y_2} + 0.25 x_1^3 y_1^3 which transformation \phi does this kernel correspond to?
Let [math: x=(x1,x2)]x=(x_1,x_2) and [math: y=(y1,y2)]y=(y_1,y_2) and let kernel k be defined as follows: [math: k(x,y)=ex1x2+y1y2+2x1y1x2y2+0.25x13y13]k(x,y) = e^{x_1x_2+y_1y_2} +2 \frac{x_1 y_1}{x_2y_2} + 0.25 x_1^3 y_1^3 which transformation [math: ϕ]\phi does this kernel correspond to?
Consider the following dataset: [math: X=[−π,−0.5π,0,0.5π,π]]X=[-\pi,-0.5\pi,0,0.5\pi,\pi] with corresponding labels [math: y=[1,−1,−1,−1,1]]y=[1,-1,-1,-1,1]. Which of the following transformations would make the data linearly separable? A. [math: ϕ(x)=(x,cos(x))]\phi(x)=(x,cos( x)) B. [math: ϕ(x)=(x,sin(x))]\phi(x)=(x,sin(x)) C. [math: ϕ(x)=(x,cos(0.5x))]\phi(x)=(x,cos(0.5 x)) D. [math: ϕ(x)=(x,sin(0.5x))]\phi(x)=(x,sin(0.5 x))
More Practical Tools for Students Powered by AI Study Helper
Making Your Study Simpler
Join us and instantly unlock extensive past papers & exclusive solutions to get a head start on your studies!