Questions
MHF4U - Quattrociocchi - S1 Unit 6 Online Quiz
Single choice
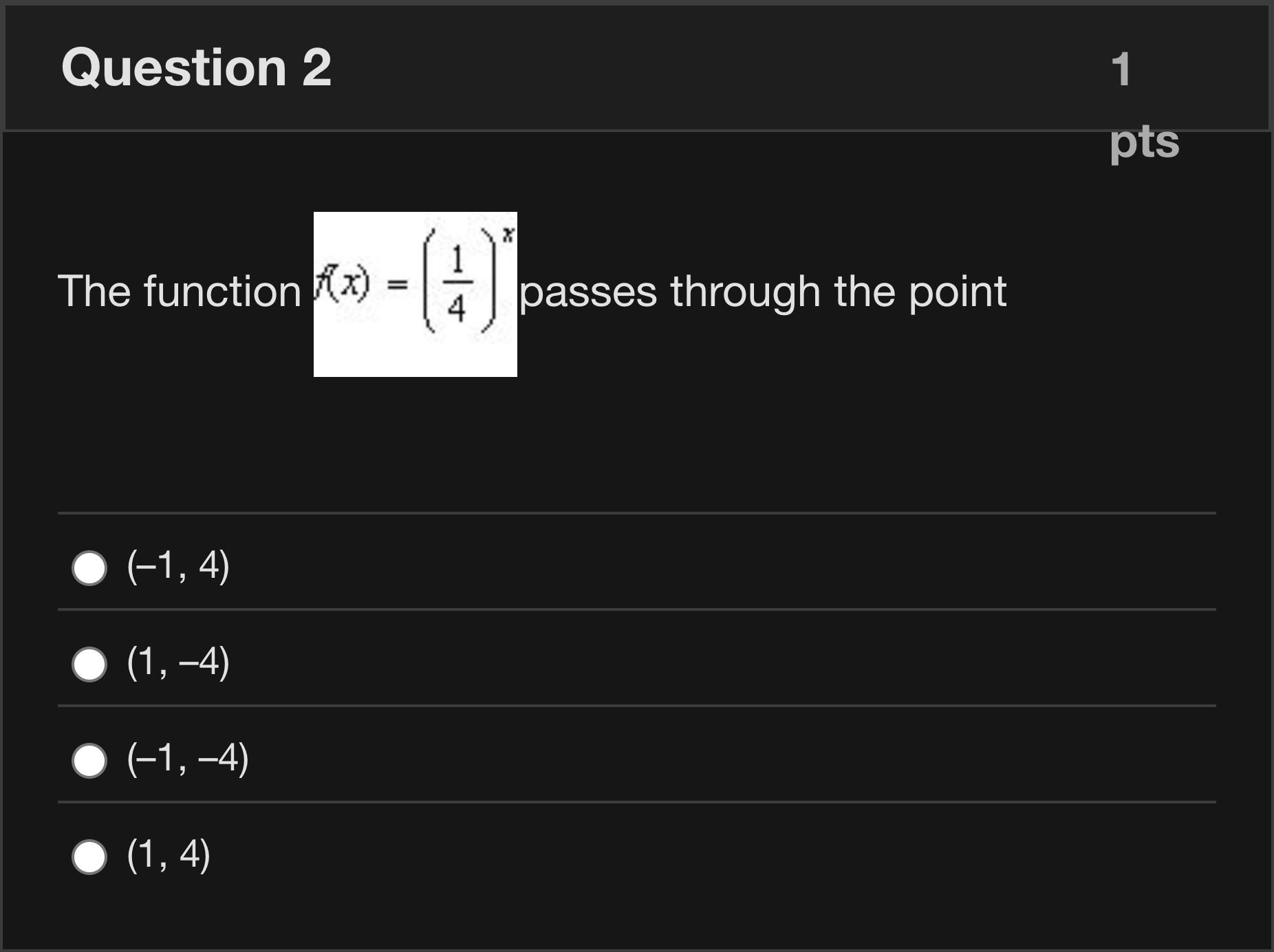
The function passes through the point
Options
A.(–1, 4)
B.(1, –4)
C.(–1, –4)
D.(1, 4)
View Explanation
Verified Answer
Please login to view
Step-by-Step Analysis
The question asks which point lies on the graph of the function given. Restating the setup: The function passes through the point, and the answer choices are the potential coordinates.
Option 1: (-1, 4). To check this, substitute x ......Login to view full explanationLog in for full answers
We've collected over 50,000 authentic exam questions and detailed explanations from around the globe. Log in now and get instant access to the answers!
Similar Questions
Part 1Determine whether the function given in the table is linear, exponential, or neither. If the function is linear, find a linear function that models the data; if it is exponential, find an exponential function that models the data. Part 1[table] x | f(x) minus−1 | nine eighths98 0 | 99 1 | 7272 2 | 576576 3 | 46084608 [/table] Part 1Select the correct choice and, if necessary, fill in the answer box to complete your choice. A. The function is exponential. An exponential function that models the data is f(x)equals=[input]enter your response here .(Simplify your answer.) B. The function is linear. A linear function that models the data is f(x)equals=[input]enter your response here .(Simplify your answer.) C. The function is neither linear nor exponential.
The function passes through the point
The exponential function for the following data set is x y 0 1 1 6 2 36 3 216 4 1296
Question at position 2 Which of the following is true? If f(x)=exf\left(x\right)=e^x, then:The domain of f is all real numbers except zero and the range is all real numbers.Both the domain and range of f are all real numbers.Both the domain and range of f are all positive real numbers.The domain of f is all real numbers and the range is all positive real numbers.The domain of f is all positive real numbers and the range is all real numbers.
More Practical Tools for Students Powered by AI Study Helper
Making Your Study Simpler
Join us and instantly unlock extensive past papers & exclusive solutions to get a head start on your studies!