Questions
Single choice
What is the domain for the function;
Options
A.a. x ∈R \ x > 1
B.b. x ∈(1,[math: ∞] \infty )\{2}
C.c. x ∈R \ 2
D.d. x ∈R \ x > 2
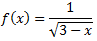
View Explanation
Verified Answer
Please login to view
Step-by-Step Analysis
To determine the domain of f(x) = 1/√(3 − x), we need the radicand to be positive (since square roots of negative numbers are not real) and we must avoid division by zero (the denominator cannot be zero). Thus, 3 − x > 0 implies x < 3, giving the domain as all real numbers less than 3.
Option a: 'a. x ∈R \ x > 1' describes all real numbers except those greater than 1, i.e., x ≤ 1. This......Login to view full explanationLog in for full answers
We've collected over 50,000 authentic exam questions and detailed explanations from around the globe. Log in now and get instant access to the answers!
Similar Questions
Part 1Find the domain of the function f(x)equals=StartFraction x squared minus 4 Over x squared minus 9 EndFractionx2−4x2−9. Part 1The domain is [input]enter your response here .(Type your answer in interval notation.)
Find the Domain Find the domain of the function. g(x)=x+3x2−81\displaystyle g\left(x\right)=\frac{x+3}{x^2-81} The domain is (−∞,(-\infty,[Fill in the blank] )∪()\cup([Fill in the blank] ,[Fill in the blank] )∪()\cup([Fill in the blank] ,∞),\infty)
Find the domain of the function. Write your answer in interval notation. Use inf for .
What is the domain of the following function? \[f(x) = \sqrt {\frac {19 x}{x^{2} - 36}}\]
More Practical Tools for Students Powered by AI Study Helper
Making Your Study Simpler
Join us and instantly unlock extensive past papers & exclusive solutions to get a head start on your studies!