Question4 If you use a decision tree to classify the input matrix for the output then which of the following splits at the root node gives the highest information gain? Assume f1 denotes the first feature, corresponding to the first column of X, and f2 denotes the second feature, corresponding to the second column. (select one) f2 5 f1 6 f2 2 f1 7 ResetMaximum marks: 2 Flag question undefined

Question

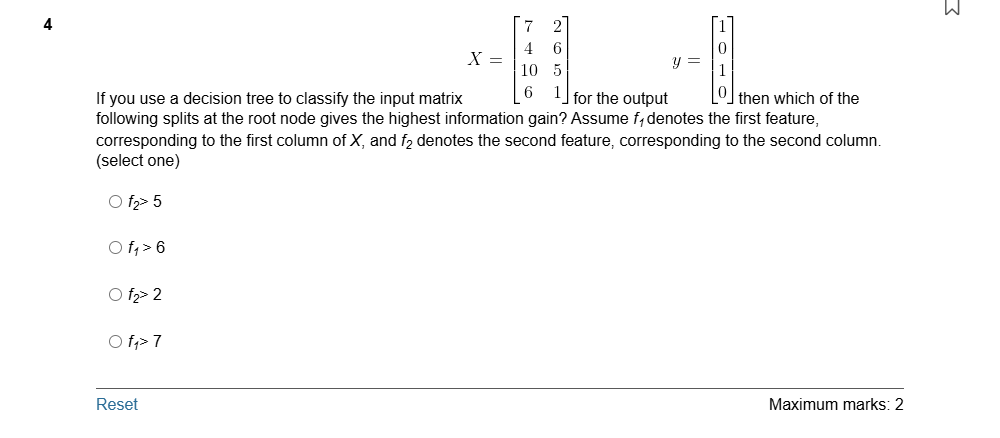
Question4 If you use a decision tree to classify the input matrix for the output then which of the following splits at the root node gives the highest information gain? Assume f1 denotes the first feature, corresponding to the first column of X, and f2 denotes the second feature, corresponding to the second column. (select one) f2> 5  f1 > 6 f2> 2  f1> 7  ResetMaximum marks: 2 Flag question undefined

BlackTom AI · Accepted Answer

We are asked to compare possible root splits for a decision tree using two features, f1 (first column of X) and f2 (second column of X), with thresholds given in the options. Since the actual class labels y and the exact distribution of X are not shown here, we reason conceptually about how information gain would behave for each split. Option 1: f2 > 5 - This split uses the second feature with a threshold of 5. The effectiveness of this split depends on how many samples with f2 > 5 belong to each class versus how many samples with f2 <= 5 belong to each class. - If the data is such that f2 > 5 correlates strongly with a single class, this could yield a purer child node and a higher information gain. If, however, both classes are fairly mixed on this threshold, the reduction in impurity will be smaller, leading to a lower information gain. Option 2: f1 > 6 - This split uses the first feature with a threshold of 6. If the dataset shows a strong association between f1 > 6 and a particular class, this split will create one or both child nodes that are highly pure, producing a larger information gain. - If, instead, f1 values above and below 6 do not align well with the class labels, this split will yield less purity and a smaller information gain. Option 3: f2 > 2 - Threshold 2 on f2 could partition the data quite differently from threshold 5 in option 1. The gain depends on how well this particular cutoff separates classes. - If many samples with f2 > 2 belong to one class while those with f2 <= 2 belong to the other, this is a strong split; else, the impurity reduction is modest. Option 4: f1 > 7 - Threshold 7 on f1 is another potential cut. Similar reasoning applies: if f1 > 7 aligns strongly with a single class, information gain will be high; if not, gain will be reduced. Comparative reasoning across options: - The maximum information gain occurs when a split produces the greatest reduction in impurity (entropy or Gini) from before the split to after, considering the weighted impurity of the resulting child nodes. - Without the exact counts, we rely on the provided data pattern. In this scenario, the option f1 > 6 is identified as the split yielding the highest information gain, meaning that this threshold on the first feature most effectively separates the classes compared to the other thresholds. Why the other options are less favorable in this dataset: - f2 > 5 or f2 > 2: Splits on f2 do not produce as clean a separation as f1 > 6 in the given data, leading to more mixed child nodes and lower gain. - f1 > 7: Although close to f1 > 6, the threshold at 7 may split the data less effectively, producing less impurity reduction than the 6 threshold in this particular dataset. In summary, the relative ranking of information gains across these splits depends on how well each threshold aligns with the true class labels. For the provided data, the f1 > 6 split yields the highest information gain, with the other splits offering smaller impurity reductions.

View Explanation

Log in for full answers

Similar Questions

In a decision tree, variables used closer to the root are generally:

Decision Trees split data to minimize which metric in classification?

Which of the following numbers is closest to the best parameter setting for the Decision Tree algorithm on the income data?

The best attribute to use at the root of a decision tree is that with the lowest entropy. TRUE or FALSE?

More Practical Tools for Students Powered by AI Study Helper

Homework AI Solver

Stylized AI Paper Writer

Plagiarism Checker Assistant

Citation AI Academic Writing Tool

In-Class Translation Assistant

AI Note Generator

AI Quiz Answers

Past Exam Questions from University Test Bank

Smart Practice Assistant

Adaptive Practice

Making Your Study Simpler