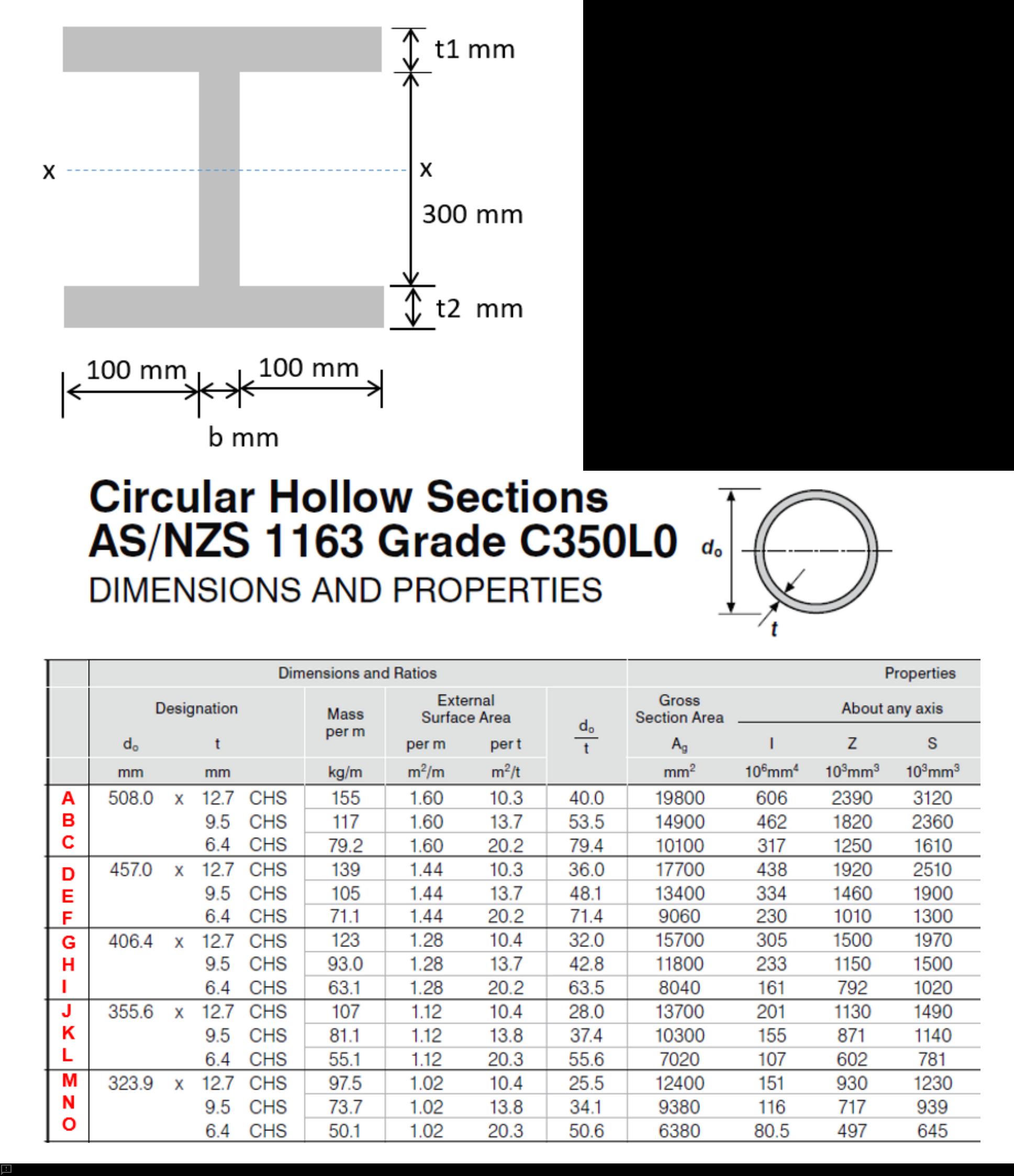
Question text 11Marks Problem 7An ‘I’ beam is shown in Figure P7.Figure P7. An I beam with dimensions.a) Assume [math: t1=t2=13]t1= t2=13 mm and [math: b=14.5] mm, making the beam now symmetrical. Calculate the second moment of area of the section, Ixx about the horizontal axis x-x. Provide your numerical answer in units of mm4 to at least 5 significant figures. [3 marks]Ixx [mm4] = Answer 1[input]b) Assume again that [math: t1=13]t1 = 13 mm and [math: b=14.5] mm BUT now [math: t2] has increased to [math: 18.2] mm . The section neutral axis now sits 151.47 mm from the base of the section and Ixx = 196798000 mm4 .  Calculate the value of the bending stress at the top of the section if a moment equal to 199 kNm is applied to the section about the horizontal axis x-x. Provide your numerical answer in units of MPa to at 2 decimal places. [3 marks]σ [MPa] = Answer 2[input]c) Where will the 'I' beam in part b) yield first in its cross-section if the applied moment continues to increase? [2 marks]Multiple choice 1at the top of the sectionat the bottom of the sectionat the neutral axissimultaneously at the top and the bottom of the section d) Assume now that the beam section is a circular hollow section that is bending. If a  maximum ultimate limit state moment of 355 kNm acts on the beam, choose the minimum weight section from Table P7 that can carry this moment without failing. [3 marks]Note; 1. Grade 350L0 represents a material yield stress of 350 MPa.Table P7: Circular Hollow Steel Section TableMultiple choice 2ABCDEFGHIJKLMNO Notes Report question issue Question 7 Notes