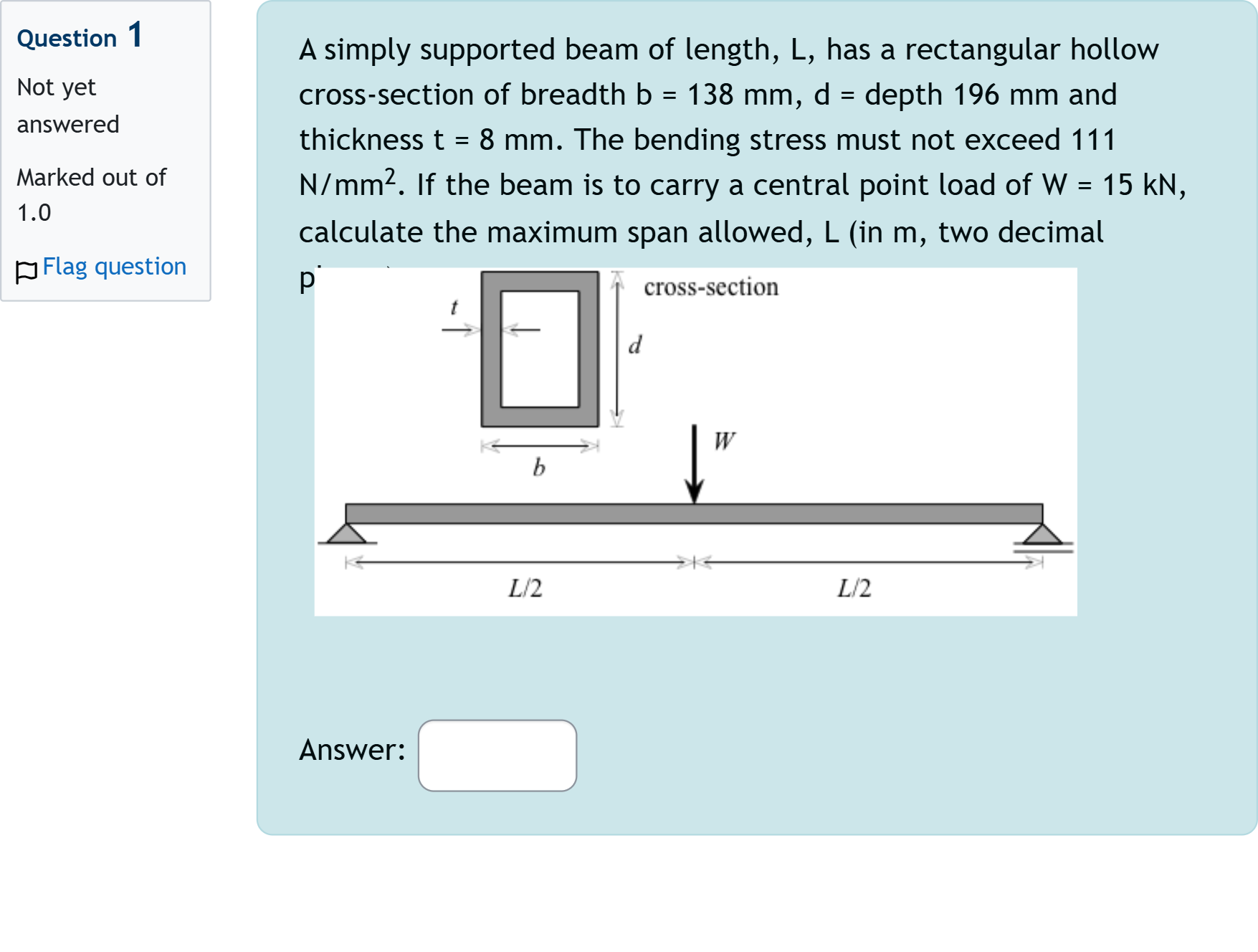
A simply supported beam of length, L, has a rectangular hollow cross-section of breadth b = 138 mm, d = depth 196 mm and thickness t = 8 mm. The bending stress must not exceed 111 N/mm2. If the beam is to carry a central point load of W = 15 kN, calculate the maximum span allowed, L (in m, two decimal places).

Question

BlackTom AI · Accepted Answer

To begin solving, I will set up the bending stress for a simply supported beam with a central point load.

- For a simply supported beam with a central load W, the maximum bending moment is Mmax = W·L/4.
- The bending stress at the outer fiber is σ = Mmax / S, where S is the section modulus of the cross-section.

Next, determine the section modulus S for the rectangular hollow cross-section.
- The outer dimensions are: breadth b_o = 138 mm and depth d_o = 196 mm.
- The inner hollow dimensions (subtracting the wall thickness t on both sides) are: breadth b_i = b_o − 2t = 138 − 16 = 122 mm, depth d_i = d_o − 2t = 196 − 16 = 180 mm.
- The second moment of area for a hollow rectangle about the horizontal centroidal axis is I = (b_o d_o^3 − b_i d_i^3)/12.
- Compute the two parts: I_o = (138)(196^3)/12 ≈ 86,589,664 mm^4 and I_i = (122)(180^3)/12 ≈ 59,292,000 mm^4.
- Therefore I = I_o − I_i ≈ 27,297,664 mm^4.
- The section modulus S for bending about the strong axis is S = I/(d/2) = I/98 (since the outer depth is 196 mm, the extreme fiber is 98 mm from the neutral axis).
- This yields S ≈ 27,297,664 / 98 ≈ 278,548 mm^3.

Apply the allowable stress condition to relate L to the given load W and allowable stress σ_allow = 111 N/mm^2.
- Set σ_allow = Mmax / S = (W·L/4) / S.
- Solve for L: L = 4·σ_allow·S / W.
- Substitute W = 15 kN = 15,000 N and the computed S: L = (4 × 111 × 278,548) / 15,000 mm.
- Numerically, 4 × 111 × 278,548 ≈ 123,675,312, and dividing by 15,000 gives L ≈ 8,245 mm.

Convert to meters: L ≈ 8,245 mm ≈ 8.25 m (two decimal places).

Summary of key steps:
- Compute inner and outer moments to get I and then S for a hollow rectangle.
- Use Mmax = W·L/4 for a central point load on a simply supported beam to relate L to allowable stress.
- Solve L = 4·σ_allow·S / W and convert units to obtain the maximum span in meters.

Dashboard ENG2081: Mechanics of Structures 2A (2025-26)

View Explanation

Log in for full answers

Similar Questions

A square section of side length [math: b] is subjected to a bending stress of [math: σ] \sigma = 5.4 MPa under a bending moment of [math: M]=6.8 kNm. Find the side length [math: b] of the square section. Provide your answer in mm, rounded to two decimal places.

In a consumer society, many adults channel creativity into buying things

More Practical Tools for Students Powered by AI Study Helper

Homework AI Solver

Stylized AI Paper Writer

Plagiarism Checker Assistant

Citation AI Academic Writing Tool

In-Class Translation Assistant

AI Note Generator

AI Quiz Answers

Past Exam Questions from University Test Bank

Smart Practice Assistant

Adaptive Practice

Making Your Study Simpler